题目内容
13. 底角为30°的等腰三角形中有垂直纸面向内的磁感应强度为B的匀强磁场,已知AD=$\frac{1}{4}$AC,现有电性不同的甲和乙两带电粒子以相同速度分别从D点沿垂直AC方向进入磁场,结果甲粒子恰好没有从EA边射出,乙粒子恰好没有从EC边射出,求:
底角为30°的等腰三角形中有垂直纸面向内的磁感应强度为B的匀强磁场,已知AD=$\frac{1}{4}$AC,现有电性不同的甲和乙两带电粒子以相同速度分别从D点沿垂直AC方向进入磁场,结果甲粒子恰好没有从EA边射出,乙粒子恰好没有从EC边射出,求:(1)甲和乙两带电粒子的比荷之比;
(2)甲和乙两带电粒子在磁场中运动时间之比.
分析 (1)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律求出粒子的比荷,然后求出比荷之比.
(2)根据粒子的周期公式求出粒子的运动时间之比.
解答 解:(1)设AD=a,则AC=4a,粒子在磁场中做圆周运动的轨道半径:
r1+r1/cos60°=a,r1=$\frac{1}{3}$a,
r2+r2/cos60°=3a,r2=a,
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,$\frac{q}{m}$=$\frac{v}{Br}$,
$\frac{\frac{{q}_{甲}}{{m}_{甲}}}{\frac{{q}_{乙}}{{m}_{乙}}}$=$\frac{\frac{v}{B{r}_{1}}}{\frac{v}{B{r}_{2}}}$=$\frac{{r}_{2}}{{r}_{1}}$=$\frac{3}{1}$;
(2)两粒子在磁场中转过的圆心角θ相等,
粒子在磁场中做圆周运动的周期:T=$\frac{2πm}{qB}$,
粒子在磁场中的运动时间之比:$\frac{{t}_{甲}}{{t}_{乙}}$=$\frac{\frac{θ}{2π}\frac{2π{m}_{甲}}{{q}_{甲}B}}{\frac{θ}{2π}\frac{2π{m}_{乙}}{{q}_{乙}B}}$=$\frac{1}{3}$;
答:(1)甲和乙两带电粒子的比荷之比为3:1;
(2)甲和乙两带电粒子在磁场中运动时间之比为1:3.
点评 本题考查了求粒子的比荷之比、运动时间之比,应用牛顿第二定律、粒子的周期公式即可正确解题.

练习册系列答案
相关题目
3. 某同学参加学校运动会立定跳远项目比赛,起跳直至着地过程如图,测量得到比赛成绩是2.5m,目测空中脚离地最大高度约0.8m,忽略空气阻力,则起跳过程该同学所做功约为( )
某同学参加学校运动会立定跳远项目比赛,起跳直至着地过程如图,测量得到比赛成绩是2.5m,目测空中脚离地最大高度约0.8m,忽略空气阻力,则起跳过程该同学所做功约为( )
 某同学参加学校运动会立定跳远项目比赛,起跳直至着地过程如图,测量得到比赛成绩是2.5m,目测空中脚离地最大高度约0.8m,忽略空气阻力,则起跳过程该同学所做功约为( )
某同学参加学校运动会立定跳远项目比赛,起跳直至着地过程如图,测量得到比赛成绩是2.5m,目测空中脚离地最大高度约0.8m,忽略空气阻力,则起跳过程该同学所做功约为( )| A. | 65J | B. | 350J | C. | 700J | D. | 1250J |
4.某宇航员在月球赤道上测得一物体的重力为F1,在月球两极测量同一物体时其重力为F2(忽略月球自转对重力的影响).则月球赤道对应的月球半径与两极处对应的月球半径之比为( )
| A. | $\frac{{F}_{1}}{{F}_{2}}$ | B. | $\frac{{F}_{2}}{{F}_{1}}$ | C. | $\sqrt{\frac{{F}_{1}}{{F}_{2}}}$ | D. | $\sqrt{\frac{{F}_{2}}{{F}_{1}}}$ |
8.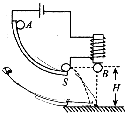 如图所示,在研究平抛运动时,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开接触开关S,被电磁铁吸住的小球B同时自由下落,改变整个装置的高度H做同样的实验,发现位于同一高度的A、B两个小球总是同时落地,该实验现象说明了A球在离开轨道后( )
如图所示,在研究平抛运动时,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开接触开关S,被电磁铁吸住的小球B同时自由下落,改变整个装置的高度H做同样的实验,发现位于同一高度的A、B两个小球总是同时落地,该实验现象说明了A球在离开轨道后( )
 如图所示,在研究平抛运动时,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开接触开关S,被电磁铁吸住的小球B同时自由下落,改变整个装置的高度H做同样的实验,发现位于同一高度的A、B两个小球总是同时落地,该实验现象说明了A球在离开轨道后( )
如图所示,在研究平抛运动时,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开接触开关S,被电磁铁吸住的小球B同时自由下落,改变整个装置的高度H做同样的实验,发现位于同一高度的A、B两个小球总是同时落地,该实验现象说明了A球在离开轨道后( )| A. | 竖直方向的分运动是匀速直线运动 | |
| B. | 竖直方向的分运动是自由落体运动 | |
| C. | 水平方向的分运动是匀加速直线运动 | |
| D. | 水平方向的分运动是匀速直线运动 |
5.对于做初速度为零的匀加速直线运动的物体,下列说法正确的是( )
| A. | 经过任意两个连续相等的距离的时间之差为常数 | |
| B. | 在相邻且相等的时间间隔内的位移之差为最初的那个时间间隔内的位移的两倍 | |
| C. | 在运动过程中,任意两个相等的时间间隔内速度的改变量相同 | |
| D. | 在运动过程中,任意两个相等的时间间隔内位移的大小之比一定是奇数 |
13. 在“探究加速度与力、质量的关系”的实验中(1)需要把木板的后墙适当垫高,以平衡小车和纸袋所受的摩擦力,对平衡摩擦力的目的,下面说法中正确的是( )
在“探究加速度与力、质量的关系”的实验中(1)需要把木板的后墙适当垫高,以平衡小车和纸袋所受的摩擦力,对平衡摩擦力的目的,下面说法中正确的是( )
 在“探究加速度与力、质量的关系”的实验中(1)需要把木板的后墙适当垫高,以平衡小车和纸袋所受的摩擦力,对平衡摩擦力的目的,下面说法中正确的是( )
在“探究加速度与力、质量的关系”的实验中(1)需要把木板的后墙适当垫高,以平衡小车和纸袋所受的摩擦力,对平衡摩擦力的目的,下面说法中正确的是( )| A. | 让小车受到的摩擦力为零 | |
| B. | 使小车所受的重力的下滑分力与所受到的摩擦阻力平衡 | |
| C. | 使小车所受的合力为零 | |
| D. | 使细线对小车的拉力等于小车所受的合外力 |
14.一个自由下落的物体,前4s下落的距离是前2s下落距离的( )
| A. | 2倍 | B. | 4倍 | C. | 6倍 | D. | 8倍 |
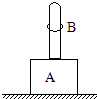 如图底座A上装有长0.5m的直立杆,其总质量M=0.2kg,杆上套有质量m=0.05kg的小环B,它与杆之间有大小恒定的摩擦力.当环从底座上以4m/s的速度飞起时刚好能到达杆顶,求(g取10m/s2):
如图底座A上装有长0.5m的直立杆,其总质量M=0.2kg,杆上套有质量m=0.05kg的小环B,它与杆之间有大小恒定的摩擦力.当环从底座上以4m/s的速度飞起时刚好能到达杆顶,求(g取10m/s2): 如图所示,两个完全相同的圆柱形常用容器,甲中装有与容器溶剂等体积的水,乙中充满空气,试问:
如图所示,两个完全相同的圆柱形常用容器,甲中装有与容器溶剂等体积的水,乙中充满空气,试问: