题目内容
11. 如图所示AB为一半径为R,在竖直平面内放置的绝缘$\frac{1}{4}$圆弧,且OA竖直,在竖直平面内施加一匀强电场,有一质量为m,电荷量为+q的小球恰能在与OA连线夹角为30°处静止.求:
如图所示AB为一半径为R,在竖直平面内放置的绝缘$\frac{1}{4}$圆弧,且OA竖直,在竖直平面内施加一匀强电场,有一质量为m,电荷量为+q的小球恰能在与OA连线夹角为30°处静止.求:(1)匀强电场的最小值;
(2)若匀强电场向水平向右且E=$\frac{mg}{q}$,将带电小球从A点静止释放,则小球的最大速度多大?
分析 小球保持静止时受到重力、电场力和圆弧的支持力,运用作图法分析什么条件下电场力最小,再场强公式E=$\frac{F}{q}$得到场强的最小值;求电场力与重力的合力,确定小球的最大速度位置,由动能定律求解.
解答 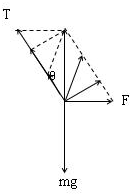 解:(1)小球保持静止时受到重力mg、电场力F和圆弧的支持力T,作出力图如图.根据作图法可知,当电场力F与圆弧的支持力T垂直时,电场力最小,最小值为:
解:(1)小球保持静止时受到重力mg、电场力F和圆弧的支持力T,作出力图如图.根据作图法可知,当电场力F与圆弧的支持力T垂直时,电场力最小,最小值为:
F=mgsinθ
则场强的最小值为:E=$\frac{F}{q}$=$\frac{mgsinθ}{q}$
(2)匀强电场向水平向右且E=$\frac{mg}{q}$,则mg与qE的合力与竖直方向夹45°斜向下,故AB弧的中点速度最大,由动能定理得:
qERsin45°-mgR(1-cos45°)=$\frac{1}{2}$mv2
解得:v=$\sqrt{2(\sqrt{2}-1)gR}$
答:(1)匀强电场的最小值$\frac{mgsinθ}{q}$;
(2)小球的最大速度$\sqrt{2(\sqrt{2}-1)gR}$
点评 本题是物体平衡中极值问题,通过作图法得到极值的条件,也可以采用数学函数法求解极值.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
2.关于功率,下列说法中正确的是( )
| A. | 功率是描述力对物体做功多少的物理量 | |
| B. | 由P=$\frac{W}{t}$可知,功率与时间成反比 | |
| C. | 由P=Fv可知,机车牵引力越大,其功率一定越大 | |
| D. | 某个力对物体做功越快,它的功率就一定越大 |
19.如图是某物体做直线运动的速度-时间图象,下列有关物体运动情况判断正确的是( )


| A. | 4s末物体回到出发点 | B. | 6s末物体距出发点最远 | ||
| C. | 8s末物体距出发点最远 | D. | 前两秒加速度为5m/s2 |
20.万有引力可以理解为:任何有质量的物体都要在其周围空间产生一个引力场,另一个有质量的物体处于这一引力场中,就受到该引力场的引力作用,这种情况可以与电场相类比,那么在地球产生的引力场中的重力加速度,可以与电场中下列哪个物理量类比( )
| A. | 电场力 | B. | 电场强度 | C. | 电势 | D. | 电势能 |
1. 如图所示,静止在水平地面上的斜面体质量为M,一质量为m的物块恰能沿斜面匀速下滑.若对物块施以水平向右的拉力F,物块m仍能沿斜面运动.则以下判断正确的是( )
如图所示,静止在水平地面上的斜面体质量为M,一质量为m的物块恰能沿斜面匀速下滑.若对物块施以水平向右的拉力F,物块m仍能沿斜面运动.则以下判断正确的是( )
 如图所示,静止在水平地面上的斜面体质量为M,一质量为m的物块恰能沿斜面匀速下滑.若对物块施以水平向右的拉力F,物块m仍能沿斜面运动.则以下判断正确的是( )
如图所示,静止在水平地面上的斜面体质量为M,一质量为m的物块恰能沿斜面匀速下滑.若对物块施以水平向右的拉力F,物块m仍能沿斜面运动.则以下判断正确的是( )| A. | 物块m将沿斜面加速下滑 | B. | 物块m仍将沿斜面匀速下滑 | ||
| C. | 地面对斜面M有向左的摩擦力 | D. | 地面对斜面的支持力等于(M+m)g |

 如图所示是做光电效应实验的装置简图.在抽成真空的玻璃管内,K为阴极(用金属铯制成,发生光电效应的逸出功为1.9eV),A为阳极.在a、b间不接任何电源,用频率为ν(高于铯的极限频率)的单色光照射阴极K,会发现电流表指针有偏转.这时,若在a、b间接入直流电源,a接正极,b接负极,并使a、b间电压从零开始逐渐增大,发现当电压表的示数增大到2.1V时,电流表的示数刚好减小到零.(普朗克恒量h=6.63×10-34J•s)
如图所示是做光电效应实验的装置简图.在抽成真空的玻璃管内,K为阴极(用金属铯制成,发生光电效应的逸出功为1.9eV),A为阳极.在a、b间不接任何电源,用频率为ν(高于铯的极限频率)的单色光照射阴极K,会发现电流表指针有偏转.这时,若在a、b间接入直流电源,a接正极,b接负极,并使a、b间电压从零开始逐渐增大,发现当电压表的示数增大到2.1V时,电流表的示数刚好减小到零.(普朗克恒量h=6.63×10-34J•s) 如图所示,电容为C、带电量为Q、极板间距为d的电容器固定在绝缘底座上,两板竖直放置,两极板及木板的总质量为M,整个装置静止在光滑水平面上.在电容器右板上有一小孔,一质量为m、带电量为+q的弹丸以速度v0从小孔水平射入电容器中(不计弹丸重力,设电容器周围电场强度为0),弹丸最远可到达距右板为x的P点,求:
如图所示,电容为C、带电量为Q、极板间距为d的电容器固定在绝缘底座上,两板竖直放置,两极板及木板的总质量为M,整个装置静止在光滑水平面上.在电容器右板上有一小孔,一质量为m、带电量为+q的弹丸以速度v0从小孔水平射入电容器中(不计弹丸重力,设电容器周围电场强度为0),弹丸最远可到达距右板为x的P点,求: