题目内容
A、B是两颗环绕地球做圆周运动的人造卫星，若两颗卫星的质量相等，环绕运动的半径rA：rB=1：3，则以下结论中正确的是（ ）A．卫星A与B的向心力之比为1：9
B．卫星A与B的向心力之比为9：1
C．卫星A与B的角速度之比为
D．卫星A与B的角速度之比为
【答案】分析：两颗质量相等的人造卫星绕同一个中心天体做圆周运动，靠万有引力提供向心力，根据F=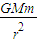
=mω2r求解
解答：解：A、人造卫星绕同一个中心天体做圆周运动，靠万有引力提供向心力，F=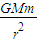
两颗卫星的质量相等，环绕运动的半径rA：rB=1：3，
卫星A与B的向心力之比为9：1．故A错误，B正确
C、
=mω2r
ω=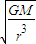
卫星A与B的角速度之比为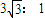
，故C正确，D错误
故选BC．
点评：解决本题的关键知道两人造卫星靠万有引力提供圆周运动的向心力，掌握线速度、角速度、加速度、周期与轨道半径的关系．
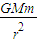=mω2r求解解答：解：A、人造卫星绕同一个中心天体做圆周运动，靠万有引力提供向心力，F=
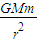
两颗卫星的质量相等，环绕运动的半径rA：rB=1：3，
卫星A与B的向心力之比为9：1．故A错误，B正确
C、
=mω2rω=
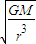
卫星A与B的角速度之比为
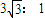，故C正确，D错误故选BC．
点评：解决本题的关键知道两人造卫星靠万有引力提供圆周运动的向心力，掌握线速度、角速度、加速度、周期与轨道半径的关系．
练习册系列答案
相关题目