题目内容
5.某人骑自行车以 4m/s的速度匀速前进,某时刻在他正前方 7m处以 10m/s的速度同向行驶的汽车开始关闭发动机,然后以大小为 2m/s2的加速度匀减速前进,求此人需多长时间才能追上汽车?分析 根据平均速度确定自行车在汽车停车前追上还是停车后追上,再根据位移时间关系求解所需时间.
解答 解:汽车做匀减速运动至停止过程中的平均速度为:
$\overline{v}$=$\frac{{v}_{0}+v}{2}$=$\frac{0+10}{2}$=5m/s>v人=4m/s,
所以人在汽车停止运动后追上;
由题意知,汽车做匀减速运动的位移:x=$\frac{{v}_{0}^{2}}{2a}$=$\frac{1{0}^{2}}{2×2}$=25m,
追上汽车时,人的位移:x人=x+7=32m,
所以人追上汽车的时间:t=$\frac{{x}_{人}}{{t}_{人}}$=$\frac{32}{4}$=8s;
答:此人需要8s才能追上汽车.
点评 掌握匀变速直线运动的位移时间关系,知道相遇时的位移关系是正确解题的关键,本题要注意判断是停车前追上还是停车后追上.

练习册系列答案
相关题目
15.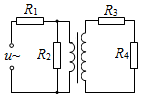 如图所示,理想变压器原、副线圈匝数比为1:2,两端分别接有四个阻值相同的定值电阻,变压器初级线圈接到交变电源上,下列说法正确的是( )
如图所示,理想变压器原、副线圈匝数比为1:2,两端分别接有四个阻值相同的定值电阻,变压器初级线圈接到交变电源上,下列说法正确的是( )
 如图所示,理想变压器原、副线圈匝数比为1:2,两端分别接有四个阻值相同的定值电阻,变压器初级线圈接到交变电源上,下列说法正确的是( )
如图所示,理想变压器原、副线圈匝数比为1:2,两端分别接有四个阻值相同的定值电阻,变压器初级线圈接到交变电源上,下列说法正确的是( )| A. | 副线圈电压是电源电压的2倍 | |
| B. | 流过R1的电流是副线圈上电流的2倍 | |
| C. | R1上的电功率是R2上电功率的2倍 | |
| D. | R1上的电功率是R2上电功率的9倍 |
16. 如图所示,A、B为两个等量同种电荷,a、0、b在点电荷A、B的连线上,C、O、d在连线的中垂线上Oa=Ob=Oc=Od,则( )
如图所示,A、B为两个等量同种电荷,a、0、b在点电荷A、B的连线上,C、O、d在连线的中垂线上Oa=Ob=Oc=Od,则( )
 如图所示,A、B为两个等量同种电荷,a、0、b在点电荷A、B的连线上,C、O、d在连线的中垂线上Oa=Ob=Oc=Od,则( )
如图所示,A、B为两个等量同种电荷,a、0、b在点电荷A、B的连线上,C、O、d在连线的中垂线上Oa=Ob=Oc=Od,则( )| A. | a、b两点的场强相同,电势也相同 | |
| B. | c、d两点的场强不相同,电势相同 | |
| C. | O点是A、B连线上电势最低的点,也是A、B连线上场强最小的点 | |
| D. | O点是中垂线cd上电势最高的点,也中垂线上场强最大的点 |
13.质量为m的滑块沿着高为h,长为l的斜面匀速下滑,在滑块从斜面顶端下滑到底端的过程中( )
| A. | 滑块克服阻力所做的功等于mgh | B. | 滑块的机械能减少mgl | ||
| C. | 合力对滑块所做的功为mgh | D. | 滑块的重力势能减少mgl |
20.关于匀变速直线运动的速度与时间关系式v=v0+at,以下的理解正确的是( )
①v0是时间间隔t开始时的速度,v是时间间隔t结束时的速度,它们均是瞬时速度
②v一定大于v0
③at是在时间间隔t内速度的变化量
④a与匀变速直线运动的v-t图象的倾斜程度无关.
①v0是时间间隔t开始时的速度,v是时间间隔t结束时的速度,它们均是瞬时速度
②v一定大于v0
③at是在时间间隔t内速度的变化量
④a与匀变速直线运动的v-t图象的倾斜程度无关.
| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
14.如图所示,一滑块放在水平长木板上,左侧拴有一细软线,跨过固定在长木板边缘的定滑轮与一重物相连,由静止释放重物后滑块在长木板上向左运动.光电门甲固定在长木板的右端,光电门乙的位置可移动,两个光电门的计时器可以显示出挡光片经过两光电门所用的时间t,每次都使滑块从同一点由静止开始运动,且滑块初始位置到光电门甲的距离L与重物初始位置到地面的距离L相等,多次改变光电门乙到光电门甲的距离X,并用米尺测量出光电门甲、乙之间的距离X,记下相应的t值,所得数据如下表所示.
请你根据题目所给数据完成下列问题:
(1)根据表中所给的数据,在坐标纸上画出$\frac{X}{t}$-t图线;
(2)根据所画出的$\frac{X}{t}$-t图线,得出滑块加速度的大小为a=3.0m/s2(结果保留两位有效数字)
(3)滑块与水平长木板之间的动摩擦因数μ=0.31(g=10m/s2)

| X(m) | 0.200 | 0.400 | 0.600 | 0.700 | 0.800 | 0.900 | 0.950 |
| t(s) | 0.088 | 0.189 | 0.311 | 0.385 | 0.473 | 0.600 | 0.720 |
| $\frac{X}{t}$(m/s) | 2.27 | 2.12 | 1.93 | 1.82 | 1.69 | 1.50 | 1.32 |
(1)根据表中所给的数据,在坐标纸上画出$\frac{X}{t}$-t图线;
(2)根据所画出的$\frac{X}{t}$-t图线,得出滑块加速度的大小为a=3.0m/s2(结果保留两位有效数字)
(3)滑块与水平长木板之间的动摩擦因数μ=0.31(g=10m/s2)

 测量液体的电阻率,工业上采用一种称为“电导仪”的仪器,其中一个关键部件如图所示,A、B是两片面积为1cm2的正方形铂片,间距为d=1cm,把它们浸在待测液体中,若通过两根引线加上一定的电压U=6V时,测出电流I=1μA,则
测量液体的电阻率,工业上采用一种称为“电导仪”的仪器,其中一个关键部件如图所示,A、B是两片面积为1cm2的正方形铂片,间距为d=1cm,把它们浸在待测液体中,若通过两根引线加上一定的电压U=6V时,测出电流I=1μA,则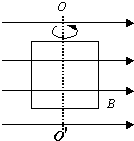 如图所示,把一个面积为4.0×10-2m2的单匝矩形线圈放在磁感应强度为2.0×10-2T的匀强磁场中,当线圈平面与磁场方向平行时,穿过线圈平面的磁通量为0Wb;当线圈绕OO′轴转动至与磁场方向垂直时,穿过线圈平面的磁通量为8×10-4Wb;在此转动过程中,穿过线圈平面的磁通量变大•(填“大”或“小”)
如图所示,把一个面积为4.0×10-2m2的单匝矩形线圈放在磁感应强度为2.0×10-2T的匀强磁场中,当线圈平面与磁场方向平行时,穿过线圈平面的磁通量为0Wb;当线圈绕OO′轴转动至与磁场方向垂直时,穿过线圈平面的磁通量为8×10-4Wb;在此转动过程中,穿过线圈平面的磁通量变大•(填“大”或“小”)