Question

如图，半径为R的光滑半圆形轨道ABC在竖直平面内，与水平轨道CD相切于C 点， D端有一被锁定的轻质压缩弹簧，弹簧左端连接在固定的挡板上，弹簧右端Q到C点的距离为2R。质量为m可视为质点的滑块从轨道上的P点由静止滑下，刚好能运动到Q点，并能触发弹簧解除锁定，然后滑块被弹回，且刚好能通过圆轨道的最高点A。已知∠POC=60°，

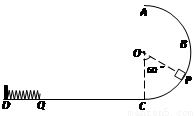
求：

（1）滑块第一次滑至圆形轨道最低点C时对轨道压力；

（2）滑块与水平轨道间的动摩擦因数μ；

（3）弹簧被锁定时具有的弹性势能。

 

Answer 1

【答案】

（1）2mg，方向竖直向下（2）0.25（3）3mgR

【解析】

试题分析：⑴设滑块第一次滑至C点时的速度为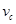,圆轨道C点对滑块的支持力为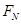

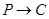过程：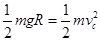  

C点：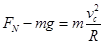        

解得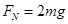           

由牛顿第三定律得：滑块对轨道C点的压力大小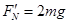，方向竖直向下 

⑵ 对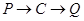过程：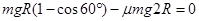 

解得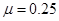              

⑶A点：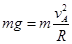        

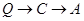过程：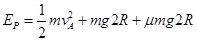

解得：弹性势能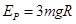      

考点：机械能守恒

点评：滑块到达Ｃ点时要看成圆周运动的开始，不能看成直线运动的结束，因为在Ｃ点滑块就受向心力作用了。