Question

（12分）如图所示，两块相同平板P₁，P₂置于光滑水平面上，质量均为m。P₂的右端固定一轻质弹簧，左端A与弹簧的自由端B相距L。物体P置于P₁的最右端，质量为2m,且可看作质点。P₁与P以共同速度v₀向右运动，与静止的P₂发生碰撞，碰撞时间极短。碰撞后P₁与P₂粘连在一起。P压缩弹簧后被弹回并停在A点（弹簧始终在弹性限度内）。P与P₂之间的动摩擦因数为μ。求

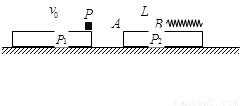
（1）P₁、P₂刚碰完时的共同速度v₁和P的最终速度v₂；

（2）此过程中弹簧的最大压缩量x和相应的弹性势能E_p。

 

Answer 1

【答案】

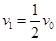
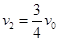（1）            （2）     

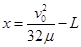
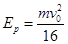
【解析】

试题分析：（1）P₁和P₂碰撞过程中，满足动量守恒定律：

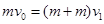          （2分）

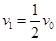解得：          （1分）

P在P₂上滑行过程， P₁、P₂、P组成的系统动量守恒：

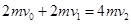          （2分）

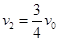解得：          （1分）

（2）P₁、P₂、P第一次速度相等，弹簧压的缩量x最大，根据能量守恒定律可得：

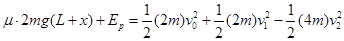        （2分）

P刚进入P₂到P₁、P₂、P第二次速度相等，根据能量守恒定律可得：

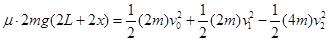           （2分）

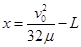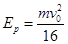解得：，       （2分）

考点：本题考查了动量守恒定律和能量守恒定律。