题目内容
15. 如图所示,在平面直角坐标系中,第一象限中有一半径为a的圆形匀强磁场区域,磁场方向垂直纸面向外,边界与两个坐标轴相切,A、B是两个阀门(控制粒子的进出),通常情况下处于关闭状态,其连线与X轴平行,B恰好位于Y轴上,坐标为(0,$a+\frac{\sqrt{2}}{2}a$)两阀门间距为d,有一粒子源发射具有沿AB方向各种速度的同一种带正电粒子(粒子所受重力不计),某时刻阀门A开启,$\frac{t}{2}$后A关闭,又过t后B开启,再过$\frac{t}{2}$后B也关闭.由两阀门通过的粒子垂直进入第一象限的圆形磁场中,其中速度最大的粒子离开磁场后,恰好能垂直通过X轴.不考虑粒子间的相互作用,求,
如图所示,在平面直角坐标系中,第一象限中有一半径为a的圆形匀强磁场区域,磁场方向垂直纸面向外,边界与两个坐标轴相切,A、B是两个阀门(控制粒子的进出),通常情况下处于关闭状态,其连线与X轴平行,B恰好位于Y轴上,坐标为(0,$a+\frac{\sqrt{2}}{2}a$)两阀门间距为d,有一粒子源发射具有沿AB方向各种速度的同一种带正电粒子(粒子所受重力不计),某时刻阀门A开启,$\frac{t}{2}$后A关闭,又过t后B开启,再过$\frac{t}{2}$后B也关闭.由两阀门通过的粒子垂直进入第一象限的圆形磁场中,其中速度最大的粒子离开磁场后,恰好能垂直通过X轴.不考虑粒子间的相互作用,求,(1)穿过A和B进入磁场的粒子的最大速度和最小速度
(2)最后离开磁场的粒子通过Y轴的坐标
(3)从第一个粒子进入磁场到最后一个粒子离开磁场经历的总时间.
分析 穿过A和B进入磁场的粒子在AB间做匀速直线运动,时间最短时速度最大,时间最长时速度最小;根据几何关系求出速度最大的和速度最小的粒子在磁场中运动半径,利用几何关系速度最大的偏转四分之一圆周垂直x轴射出,速度最小的偏转二分之一圈垂直y轴射出:第三问以B打开为计时起点,最快的正好B,最慢的还需要$\frac{t}{2}$到达B,计算出最快的到达磁场时间,最慢的从打开B到离开磁场的时间,两者之差即是所求时间.
解答 解:(1)A关闭时进入,B打开时通过的粒子具有最大速度,${v}_{1}^{\;}=\frac{d}{t}$
A打开时通过,B关闭时通过的粒子具有最小速度${v}_{2}^{\;}=\frac{d}{2t}$
(2)速度最大的粒子恰好垂直通过x轴,在磁场中运动的几何半径为:${R}_{1}^{\;}=\sqrt{2}a$
根据:$Bqv=m\frac{{v}_{\;}^{2}}{R}$
可得:最小速度的粒子在磁场中运动的半径为:${R}_{2}^{\;}=\frac{\sqrt{2}a}{2}$
由几何关系可得,粒子恰好垂直y轴射出,其坐标为(0,$a-\frac{\sqrt{2}a}{2}$)
(3)设B打开时为零时刻,最快粒子到达磁场需要时间:${t}_{1}^{\;}=\frac{a-\frac{\sqrt{2}}{2}a}{d}t$
最慢粒子由B到达磁场所用时间:${t}_{2}^{\;}=\frac{a-\frac{\sqrt{2}}{2}a}{d}2t$
最慢粒子在磁场中运动的时间:${t}_{3}^{\;}=\frac{\frac{\sqrt{2}}{2}πa}{d}2t$
第一个粒子进入磁场到最后一个粒子离开磁场经历的总时间
$△t=\frac{t}{2}+{t}_{2}^{\;}+{t}_{3}^{\;}-{t}_{1}^{\;}$
得:$△t=\frac{t}{2}+\frac{a}{d}(1-\frac{\sqrt{2}}{2}+\sqrt{2}π)t$
答:(1)穿过A和B粒子的最大速度$\frac{d}{t}$,最小速度$\frac{d}{2t}$
(2)最后通过磁场的粒子通过Y轴的坐标(0,$a-\frac{\sqrt{2}a}{2}$)
(3)第一个粒子进入磁场到最后一个粒子离开磁场经历的总时间$\frac{t}{2}+\frac{a}{d}(1-\frac{\sqrt{2}}{2}+\sqrt{2}π)t$
点评 本题是带电粒子在匀强磁场中运动的问题,分析粒子的受力情况,确定其运动情况,第三问比较难,关键是要理清运动的过程,弄清物理情景.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案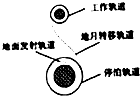 中国月球探测卫星“嫦娥号”简化后的路线示意图如图所示,卫星由地面发射后,先经过地面发射轨道进入地球附近的停泊轨道做匀速圆周运动;然后从停泊轨道经过调控进入地月转移轨道;到达月球附近时,再次调控进入工作轨道做匀速圆周运动,这时卫星将开始对月球进行探测.已知地球与月球的质量之比为a,卫星的停泊轨道与工作轨道的轨道半径之比为b.则下列说法中正确的是( )
中国月球探测卫星“嫦娥号”简化后的路线示意图如图所示,卫星由地面发射后,先经过地面发射轨道进入地球附近的停泊轨道做匀速圆周运动;然后从停泊轨道经过调控进入地月转移轨道;到达月球附近时,再次调控进入工作轨道做匀速圆周运动,这时卫星将开始对月球进行探测.已知地球与月球的质量之比为a,卫星的停泊轨道与工作轨道的轨道半径之比为b.则下列说法中正确的是( )| A. | 卫星从停泊轨道调控进入到地月转移轨道的过程中,卫星的机械能不守恒 | |
| B. | 卫星在停泊轨道运行的速度可能大于地球的第一宇宙速度 | |
| C. | 卫星在停泊轨道和工作轨道运行的线速度大小之比为$\sqrt{b}$:$\sqrt{a}$ | |
| D. | 卫星在停泊轨道和工作轨道运行的周期之比为b$\sqrt{b}$:$\sqrt{a}$ |
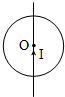 如图,一根长直导线竖直放置,通以向上的电流.直导线与铜圆环紧贴但相互绝缘,且导线经过环心O.下述各过程中,铜环中有感应电流的是( )
如图,一根长直导线竖直放置,通以向上的电流.直导线与铜圆环紧贴但相互绝缘,且导线经过环心O.下述各过程中,铜环中有感应电流的是( )| A. | 环竖直向上匀速运动 | B. | 环绕环心O匀速转动 | ||
| C. | 环向左匀速运动 | D. | 环以导线为轴匀速转动 |
| A. | 肥皂泡呈现的彩色是光的干涉现象,露珠呈现的彩色是光的色散现象,通过狭缝看太阳光呈现的彩色是光的衍射现象 | |
| B. | 刮胡须的刀片的影子边缘模糊不清是光的衍射现象 | |
| C. | 全息照相、光纤通信及医用纤维式内窥镜都是利用了光的全反射原理 | |
| D. | 光的偏振现象说明光是横波 | |
| E. | X射线比无线电波更容易发生干涉和衍射现象 |
| A. | 物体对支持面的压力越大,摩擦力也越大 | |
| B. | 所有物体弹力的大小都与物体的弹性形变的大小成正比 | |
| C. | 静止的物体不可能受到滑动摩擦力的作用 | |
| D. | 通常所说的压力、拉力、支持力等都是接触力,它们在本质上都是电磁相互作用 |
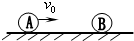 如图所示,在光滑的水平面上,质量为m的小球A以速率v0向右运动时与静止的等质量的小球B发生碰撞,碰后两球粘在一起,则碰后两球的速率v=$\frac{{v}_{0}}{2}$;碰撞过程中损失的机械能△E=$\frac{1}{4}m{v}_{0}^{2}$.
如图所示,在光滑的水平面上,质量为m的小球A以速率v0向右运动时与静止的等质量的小球B发生碰撞,碰后两球粘在一起,则碰后两球的速率v=$\frac{{v}_{0}}{2}$;碰撞过程中损失的机械能△E=$\frac{1}{4}m{v}_{0}^{2}$. 在如图所示的圆锥摆中,已知小球质量为m,绳子长度为L,绳子转动过程中与竖直方向的夹角为θ,试求:
在如图所示的圆锥摆中,已知小球质量为m,绳子长度为L,绳子转动过程中与竖直方向的夹角为θ,试求: