题目内容
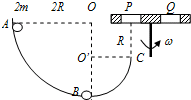 如图,半径为2R的
如图,半径为2R的| 1 |
| 4 |
| 1 |
| 4 |
(1)两球第一次碰撞后2球的速度大小
(2)欲使2球能从小孔Q落下,则平台的角速度ω 应满足什么条件?(不计所有阻力)
分析:(1)先根据动能定理求得小球1从A点处滑至B点时的速度.两球发生的是弹性碰撞,满足动量守恒和机械能守恒,根据两大守恒定律列式求解两球第一次碰撞后2球的速度大小.
(2)求出小球2在空中的运动时间,由平台转动的周期性,再求解平台的角速度ω 应满足什么条件.
(2)求出小球2在空中的运动时间,由平台转动的周期性,再求解平台的角速度ω 应满足什么条件.
解答:解:(1)设小球1在B点速度大小为v0,则根据动能定理得:
2mg?2R=
?2mv02-0
解得:v0=2
两球碰撞过程满足动量守恒和机械能守恒,设两球碰后速度大小为v1和v2,取碰撞前球1的速度方向为正方向,则:2mv0=2mv1+mv2
且
?2mv02=
?2mv12+
?mv22
所以:v2=
v0=
; v1=
v0=
(2)对碰后B球上升至P的过程,由机械能守恒得:
mv22=
mvP2+2mgR
解得:vP=
而小球做竖直上抛的时间满足:t=
又因为t=
(k=0,1,2,3…)
所以角速度ω=
=
,(k=0,1,2,3…)
答:(1)两球第一次碰撞后2球的速度大小为2
.
(2)欲使2球能从小孔Q落下,则平台的角速度ω 应满足ω=
,(k=0,1,2,3…).
2mg?2R=
| 1 |
| 2 |
解得:v0=2
| gR |
两球碰撞过程满足动量守恒和机械能守恒,设两球碰后速度大小为v1和v2,取碰撞前球1的速度方向为正方向,则:2mv0=2mv1+mv2
且
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以:v2=
| 4 |
| 3 |
| 8 |
| 3 |
| gR |
| 1 |
| 3 |
2
| ||
| 3 |
(2)对碰后B球上升至P的过程,由机械能守恒得:
| 1 |
| 2 |
| 1 |
| 2 |
解得:vP=
| 2 |
| 3 |
| 7gR |
而小球做竖直上抛的时间满足:t=
| 2vp |
| g |
又因为t=
| (2k+1)π |
| ω |
所以角速度ω=
| (2k+1)π |
| t |
3(2k+1)π
| ||
| 28R |
答:(1)两球第一次碰撞后2球的速度大小为2
| gR |
(2)欲使2球能从小孔Q落下,则平台的角速度ω 应满足ω=
3(2k+1)π
| ||
| 28R |
点评:分析研究对象的运动过程是解决动力学问题的前提,根据题目已知条件和求解的物理量选择物理规律解决问题.本题关键要抓住圆周运动的周期性得到角速度的表达式,不能当作特殊值去求.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
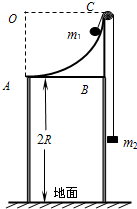 如图,半径为R的1/4圆弧支架竖直放置,支架底AB离地的距离为2R,圆弧边缘C处有一小定滑轮,一轻绳两端系着质量分别为m1与m2的物体,挂在定滑轮两边,且m1>m2,开始时m1、m2均静止,m1、m2可视为质点,不计一切摩擦.求:
如图,半径为R的1/4圆弧支架竖直放置,支架底AB离地的距离为2R,圆弧边缘C处有一小定滑轮,一轻绳两端系着质量分别为m1与m2的物体,挂在定滑轮两边,且m1>m2,开始时m1、m2均静止,m1、m2可视为质点,不计一切摩擦.求:

