题目内容
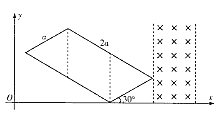
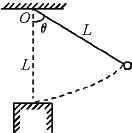
【题目】如图所示,某物体自空间O点以水平初速度![]() 抛出,落在地面上的A点,其轨迹为一抛物线。现仿此抛物线制作一个光滑滑道并固定在与OA完全重合的位置上,然后将此物体从O点由静止释放,受微小扰动而沿此滑道滑下,在下滑过程中物体未脱离滑道。P为滑道上一点,OP连线与竖直方向成45°角,则此物体
抛出,落在地面上的A点,其轨迹为一抛物线。现仿此抛物线制作一个光滑滑道并固定在与OA完全重合的位置上,然后将此物体从O点由静止释放,受微小扰动而沿此滑道滑下,在下滑过程中物体未脱离滑道。P为滑道上一点,OP连线与竖直方向成45°角,则此物体

A.物体经过P点时,速度的水平分量为![]()
B.由O运动到P点的时间为![]()
C.物体经过P点时,速度的竖直分量为![]()
D.物体经过P点时的速度大小为![]()
【答案】A
【解析】
考查平抛运动的规律。
ACD.从O到P点,平抛运动时,根据几何关系:

运动时间:
![]()
竖直位移:
![]()
速度与水平夹角
![]()
沿滑道设到P点速度为v,根据动能定理得:
![]()
解得:![]()
设水平分速度![]() ,竖直分速度
,竖直分速度![]() ,所以
,所以![]() ,根据勾股定理可知:
,根据勾股定理可知:
![]()
解得![]() ,A正确CD错误;
,A正确CD错误;
B.平抛时,竖直方向自由落体,时间:
![]()
沿滑道下滑时,竖直方向由于受到支持力,合外力小于重力,加速度小于重力加速度,所以时间长,B错误。
故选A。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目