题目内容
14.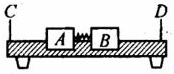 如图所示,气垫导轨是常用的一种实验仪器.它是利用气泵使带孔的导轨与滑块之间形成气垫,使滑块悬浮在导轨上,滑块在导轨上的运动可视为没有摩擦.我们可以用带竖直挡板C、D的气垫导轨以及滑块A、B来验证动量守恒定律,实验装置如图所示(弹簧的长度忽略不计),采用的实验步骤如下:
如图所示,气垫导轨是常用的一种实验仪器.它是利用气泵使带孔的导轨与滑块之间形成气垫,使滑块悬浮在导轨上,滑块在导轨上的运动可视为没有摩擦.我们可以用带竖直挡板C、D的气垫导轨以及滑块A、B来验证动量守恒定律,实验装置如图所示(弹簧的长度忽略不计),采用的实验步骤如下:(a)用天平分别测出滑块A、B的质量mA、mB.
(b)调整气垫导轨,使导轨处于水平.
(c)在滑块A、B间放入一个被压缩的轻弹簧用电动卡销锁定,静止放置在气垫导轨上.
(d)用刻度尺测出滑块A的左端至板C的距离L1.
(e)按下电钮放开卡销,同时使分别记录滑块A、B运动时间的计时器开始工作.当滑块A、B分别碰撞挡板C、D时停止计时,计下滑块A、B分别到达挡板C、D的运动时间t1和t2.
(1)实验中还应测量的物理量是B的右端至D板的距离L2..
(2)利用上述测量的实验数据,验证动量守恒定律的表达式是mA$\frac{{L}_{1}}{{t}_{1}}$-mB$\frac{{L}_{2}}{{t}_{2}}$=0.,由此公式算得的A、B两滑块的动量大小并不完全相等,产生误差的原因是测量时间、距离等存在误差,由于阻力、气垫导轨不水平等造成误差..
(3)利用上述实验数据能否测出被压缩弹簧的弹性势能的大小?如能,请写出表达式.如不能,说明理由.能测出被压缩弹簧的弹性势能,EP=$\frac{1}{2}{m}_{A}$$\frac{{{L}_{1}}^{2}}{{{t}_{1}}^{2}}$+$\frac{1}{2}$mB$\frac{{{L}_{2}}^{2}}{{{t}_{2}}^{2}}$..
分析 (1)要验证动量守恒定律需要知道物体的质量和速度,而速度可以用位移与时间的比值代替,故要测位移;
(2)利用vA=$\frac{{L}_{1}}{{t}_{1}}$,VB=$\frac{{L}_{2}}{{t}_{2}}$,即可将mAvA-mBVB=0,转化为mA$\frac{{L}_{1}}{{t}_{1}}$-mB$\frac{{L}_{2}}{{t}_{2}}$=0.
(3)根据能量守恒,弹簧的弹性势能转化为两滑块匀速运动时的动能即Ep=$\frac{1}{2}{m}_{A}{{V}_{A}}^{2}$+$\frac{1}{2}{m}_{B}\;{{v}_{B}}^{2}$,利用位移求出vA和vB.
解答 解:(1)因系统水平方向动量守恒即mAvA-mBVB=0,由于系统不受摩擦,故滑块在水平方向做匀速直线运动故有vA=$\frac{{L}_{1}}{{t}_{1}}$,VB=$\frac{{L}_{2}}{{t}_{2}}$,即mA$\frac{{L}_{1}}{{t}_{1}}$-mB$\frac{{L}_{2}}{{t}_{2}}$=0.
所以还要测量的物理量是:B的右端至D板的距离L2.
(2)由(1)分析可知验证动量守恒定律的表达式是mA$\frac{{L}_{1}}{{t}_{1}}$-mB$\frac{{L}_{2}}{{t}_{2}}$=0.
本实验中的误差主要来自由测量时间、距离等存在误差;同时由于阻力不能忽略;气垫导轨不水平等均要造成误差.
(3)根据能量守恒定律被压缩弹簧的弹性势能Ep=$\frac{1}{2}{m}_{A}{{V}_{A}}^{2}$+$\frac{1}{2}{m}_{B}\;{{v}_{B}}^{2}$,
将vA=$\frac{{L}_{1}}{{t}_{1}}$,VB=$\frac{{L}_{2}}{{t}_{2}}$代入上式得EP=$\frac{1}{2}{m}_{A}$$\frac{{{L}_{1}}^{2}}{{{t}_{1}}^{2}}$+$\frac{1}{2}$mB$\frac{{{L}_{2}}^{2}}{{{t}_{2}}^{2}}$.
故本题的答案为:(1)B的右端至D板的距离L2.
(2)mA$\frac{{L}_{1}}{{t}_{1}}$-mB$\frac{{L}_{2}}{{t}_{2}}$=0.测量时间、距离等存在误差,由于阻力、气垫导轨不水平等造成误差.
(3)能测出被压缩弹簧的弹性势能,EP=$\frac{1}{2}{m}_{A}$$\frac{{{L}_{1}}^{2}}{{{t}_{1}}^{2}}$+$\frac{1}{2}$mB$\frac{{{L}_{2}}^{2}}{{{t}_{2}}^{2}}$
点评 本题考查动量守恒定律的验证;利用位移或位移与时间的比值表示物体的速度是物理实验中常用的一种方法,要注意掌握

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案| A. | N向下运动插入线圈 | B. | S极向下运动插入线圈 | ||
| C. | N极向上从线圈中拔出 | D. | 静止在线圈中不动 |
 如图所示,不计电阻的光滑U形金属框水平放置,光滑、竖直玻璃挡板H、P固定在框上,H、P的间距很小.质量为0.2kg的细金属杆CD恰好无挤压地放在两挡板之间,与金属框接触良好并围成边长为1m的正方形,其有效电阻为0.1Ω.此时在整个空间加方向与水平面成30°角且与金属杆垂直的匀强磁场,磁感应强度随时间变化规律是B=(0.4-0.2t)T,图示磁场方向为正方向.框、挡板和杆不计形变.则( )
如图所示,不计电阻的光滑U形金属框水平放置,光滑、竖直玻璃挡板H、P固定在框上,H、P的间距很小.质量为0.2kg的细金属杆CD恰好无挤压地放在两挡板之间,与金属框接触良好并围成边长为1m的正方形,其有效电阻为0.1Ω.此时在整个空间加方向与水平面成30°角且与金属杆垂直的匀强磁场,磁感应强度随时间变化规律是B=(0.4-0.2t)T,图示磁场方向为正方向.框、挡板和杆不计形变.则( )| A. | t=1s时,金属杆中感应电流方向从C至D | |
| B. | t=3s时,金属杆中感应电流方向从D至C | |
| C. | t=1s时,金属杆对挡板P的压力大小为0.1N | |
| D. | t=3s时,金属杆对挡板H的压力大小为1.2N |
| A. | 当P点向上通过平衡位置时,Q点将从波峰开始向下运动 | |
| B. | 当P点从波峰开始向下运动时,Q点将从波谷开始向上运动 | |
| C. | 当P点向下通过平衡位置时,Q点将从波谷开始向上运动 | |
| D. | 当P点从波谷开始向上运动时,Q点将向上通过平衡位置 |

| A. | 在水中a光的速度比b光的速度小 | |
| B. | 从水射向空气时a光的临界角大于b光的临界角 | |
| C. | 用同一双缝干涉实验装置分别以a、b光做实验,它们的干涉条纹宽度不是均匀的 | |
| D. | 用同一双缝干涉实验装置分别以a、b光做实验,a光的干涉条纹间距大于b光的干涉条纹间距 |

 两个小球固定在一根长为L的杆的两端,它们绕杆上的O 点在水平面上作匀速圆周运动,如图所示,如果小球1的质量为m1,线速度为v1,小球2的质量为m2,线速度为v2,求:
两个小球固定在一根长为L的杆的两端,它们绕杆上的O 点在水平面上作匀速圆周运动,如图所示,如果小球1的质量为m1,线速度为v1,小球2的质量为m2,线速度为v2,求: