题目内容
6. 两个小球固定在一根长为L的杆的两端,它们绕杆上的O 点在水平面上作匀速圆周运动,如图所示,如果小球1的质量为m1,线速度为v1,小球2的质量为m2,线速度为v2,求:
两个小球固定在一根长为L的杆的两端,它们绕杆上的O 点在水平面上作匀速圆周运动,如图所示,如果小球1的质量为m1,线速度为v1,小球2的质量为m2,线速度为v2,求:(1)转轴O到小球2的距离R2为多少?
(2)小球1受到杆对它的拉力是多少?
分析 (1)两球共轴转动,角速度相等,根据公式v=rω求出转动的半径之比,从而结合杆子的长度求出转轴O到小球2的距离.
(2)拉力提供向心力,根据F=m$\frac{{v}^{2}}{R}$求解拉力.
解答 解:(1)两球的角速度相等,根据v=rω知:
$\frac{{R}_{1}}{{R}_{2}}=\frac{{v}_{1}}{{v}_{2}}$ ①
由于:
R1+R2=L ②
联立解得:
R1=$\frac{{v}_{1}L}{{v}_{1}+{v}_{2}}$
R2=$\frac{{v}_{2}L}{{v}_{1}+{v}_{2}}$
(2)对于小球1,拉力提供向心力,故:
F=${m}_{1}\frac{{v}_{1}^{2}}{{R}_{1}}$=$\frac{{m}_{1}{v}_{1}({v}_{1}+{v}_{2})}{L}$
答:(1)转轴O到小球2的距离R2为$\frac{{v}_{2}L}{{v}_{1}+{v}_{2}}$;
(2)小球1受到杆对它的拉力是$\frac{{m}_{1}{v}_{1}({v}_{1}+{v}_{2})}{L}$.
点评 解决本题的关键知道两球的角速度相等,通过线速度之比得出转动的半径之比是本题的突破口,还要记住向心力公式.

练习册系列答案
相关题目
17.某简谐振子,自由振动时的振动图象如甲图中实线所示,而在某驱动力作用下作受迫振动时,稳定后的振动图象如甲图中虚线所示,那么,此受迫振动对应的状态可能是图乙中的( )


| A. | a点 | B. | b点 | C. | c点 | D. | 一定不是c点 |
17.用细线拴住一个小球在光滑的水平面内做匀速圆周运动,下列描述小球运动的物理量,发生变化的是( )
| A. | 转速 | B. | 线速度 | C. | 周期 | D. | 角速度 |
15. 如图所示,两人各用6N的力沿相反方向拉一轻质弹簧的两端.当弹簧静止时,它所受的弹力和合力大小分别是( )
如图所示,两人各用6N的力沿相反方向拉一轻质弹簧的两端.当弹簧静止时,它所受的弹力和合力大小分别是( )
 如图所示,两人各用6N的力沿相反方向拉一轻质弹簧的两端.当弹簧静止时,它所受的弹力和合力大小分别是( )
如图所示,两人各用6N的力沿相反方向拉一轻质弹簧的两端.当弹簧静止时,它所受的弹力和合力大小分别是( )| A. | 6N,0N | B. | 12N,12N | C. | 12N,0N | D. | 6N,6N |
16.下列结论正中确的是( )
| A. | 均匀变化电场在它的周围产生均匀变化的磁场 | |
| B. | 电磁波中每一处的电场强度和磁场强度总是相互垂直的,且与波的传播方向垂直 | |
| C. | 电磁波频率越高,在真空中传播速度越大 | |
| D. | 机械波的传播需要介质,电磁波可以在真空中传播 |
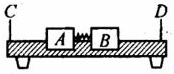 如图所示,气垫导轨是常用的一种实验仪器.它是利用气泵使带孔的导轨与滑块之间形成气垫,使滑块悬浮在导轨上,滑块在导轨上的运动可视为没有摩擦.我们可以用带竖直挡板C、D的气垫导轨以及滑块A、B来验证动量守恒定律,实验装置如图所示(弹簧的长度忽略不计),采用的实验步骤如下:
如图所示,气垫导轨是常用的一种实验仪器.它是利用气泵使带孔的导轨与滑块之间形成气垫,使滑块悬浮在导轨上,滑块在导轨上的运动可视为没有摩擦.我们可以用带竖直挡板C、D的气垫导轨以及滑块A、B来验证动量守恒定律,实验装置如图所示(弹簧的长度忽略不计),采用的实验步骤如下: