题目内容
7. 如图所示,竖直放置的平行金属板,板间电压为U0.质量为m,电量为q的带正电的粒子(不计重力)自左极板的a处由静止释放,加速后从右极板的小孔b射出.由o点垂直于mf边的方向射入边长为L的正方形场区,o为mf边的中点.
如图所示,竖直放置的平行金属板,板间电压为U0.质量为m,电量为q的带正电的粒子(不计重力)自左极板的a处由静止释放,加速后从右极板的小孔b射出.由o点垂直于mf边的方向射入边长为L的正方形场区,o为mf边的中点.(1)若正方形区域内仅存在垂直于mn方向的匀强电场,求电场强度E多大能使粒子从n点射出场区;
(2)若正方形区域内仅存在垂直于纸面方向的匀强磁场,求磁感应强度B大小满足什么条件能使粒子从m、n两点间射出场区.
分析 (1)若只有电场时,带电粒子在电场中做类平抛运动,由运动的合成与分解可求得E的大小;
(2)若存在磁场时,根据几何关系可确定半径的范围,再由洛仑兹力充当向心力可求得B的范围.
解答 解:(1)由动能定理可得:
U0q=$\frac{1}{2}$mv20
只电场时,带电粒子在正方形区域内做类平抛运动;
水平方向有:L=v0t;
竖直方向$\frac{L}{2}$=$\frac{1}{2}$at2=$\frac{1}{2}×\frac{Eq}{m}$t2;
联立解得:E=$\frac{2{U}_{0}}{L}$;
(2)要使粒子从m点穿出,粒子的转动半径为$\frac{L}{4}$;
要使粒子从n点穿出,由几何关系可知:
R2-(R-$\frac{L}{2}$)2=L2;
解得:R=$\frac{5L}{4}$;
即半径满足条件为:$\frac{L}{4}$≤R$≤\frac{5L}{4}$
由洛仑兹力充当向心力可知:
Bqv0=$\frac{m{{v}_{0}}^{2}}{r}$
解得:B=$\frac{m{v}_{0}}{qR}$
因v0=$\sqrt{\frac{2q{U}_{0}}{m}}$
则有B=$\frac{1}{R}$$\sqrt{\frac{2m{U}_{0}}{q}}$;
则B的范围为:$\frac{4}{5L}\sqrt{\frac{2m{U}_{0}}{q}}$≤B≤$\frac{4}{L}×\sqrt{\frac{2m{U}_{0}}{q}}$
答:(1)电场强度为$\frac{2{U}_{0}}{L}$时,可以从n点穿出;
(2)当B满足$\frac{4}{5L}\sqrt{\frac{2m{U}_{0}}{q}}$≤B≤$\frac{4}{L}×\sqrt{\frac{2m{U}_{0}}{q}}$时,带电粒子从mn间穿出.
点评 本题考查带电粒子在电场和磁场中的运动,要注意明确带电粒子在电场中做类平抛运动,在磁场中做匀速圆周运动.

 备战中考寒假系列答案
备战中考寒假系列答案 如图所示,一通电圆环质量为m,电流方向为逆时针方向放在水平桌面上,一条形磁铁竖直放在环的中心处,N极在下端,下面判断正确的是( )
如图所示,一通电圆环质量为m,电流方向为逆时针方向放在水平桌面上,一条形磁铁竖直放在环的中心处,N极在下端,下面判断正确的是( )| A. | 环对桌面的压力仍为mg | B. | 环对桌面的压力小于mg | ||
| C. | 环对桌面的压力大于mg | D. | 环所受桌面对它的摩擦力为零 |
 如图所示,将倾角为α的粗糙斜面体置于水平地面上,斜面体上有一木块,对木块施加一斜向上的拉力F,整个系统处于静止状态,下列说法正确的是( )
如图所示,将倾角为α的粗糙斜面体置于水平地面上,斜面体上有一木块,对木块施加一斜向上的拉力F,整个系统处于静止状态,下列说法正确的是( )| A. | 木块和斜面体间可能无摩擦 | |
| B. | 木块和斜面体间一定有摩擦 | |
| C. | 斜面体和水平地面间可能无摩擦 | |
| D. | 撤掉拉力F后,斜面体和水平地面间一定有摩擦 |
 在光滑的水平面上有两个质量均为m的物块A和B,物块B的左端与一轻弹簧相连并处于静止状态,如图所示.物块A以速度v0向物块B运动,在物块A通过弹簧和物块B相互作用的过程中,下列说法正确的是( )
在光滑的水平面上有两个质量均为m的物块A和B,物块B的左端与一轻弹簧相连并处于静止状态,如图所示.物块A以速度v0向物块B运动,在物块A通过弹簧和物块B相互作用的过程中,下列说法正确的是( )| A. | 弹簧对物块A和对物块B的冲量相同 | |
| B. | 物块A、弹簧和物块B组成的系统,机械能不守恒 | |
| C. | 弹簧的最大弹性势能为$\frac{1}{4}$mv02 | |
| D. | 物块B获得的最大速度可能大于v0 |
| A. | 8N | B. | 16N | C. | 0 | D. | 9.6N |
| A. | 提升过程中物体重力势能减少mgh | B. | 提升过程中合力对物体做功mah | ||
| C. | 提升过程中物体的动能增加m(g+a)h | D. | 提升过程中物体重力势能增加mgh |


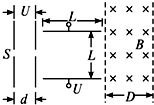 如图所示,在S点的电荷量为q、质量为m的静止带电粒子,被加速电压为U、极板间距离为d的匀强电场加速后,从正中央垂直射入电压为U的匀强偏转电场,偏转极板长度和极板距离均为L.(不计重力影响)
如图所示,在S点的电荷量为q、质量为m的静止带电粒子,被加速电压为U、极板间距离为d的匀强电场加速后,从正中央垂直射入电压为U的匀强偏转电场,偏转极板长度和极板距离均为L.(不计重力影响)