题目内容
19. 科学工作者常常用介质来显示带电粒子的径迹.如图所示,平面内存在着垂直于纸面向外的匀强磁场,磁感应强度B=4×10-2T.x轴上方真空,x轴下方充满某种不导电的介质并置于沿x轴方向的匀强电场中,粒子在介质中运动时会受到大小为f=kv粘滞阻力,y轴上P(0,0.08)点存在一个粒子源,能沿纸面向各个方向发射质量m=1.6×10-25kg、带电量q=+1.6×10-19C且进入介质中,观察到该粒子在介质中的径迹为直线(不计重力及粒子间下滑作用,粒子在介质中运动时电量不变).
科学工作者常常用介质来显示带电粒子的径迹.如图所示,平面内存在着垂直于纸面向外的匀强磁场,磁感应强度B=4×10-2T.x轴上方真空,x轴下方充满某种不导电的介质并置于沿x轴方向的匀强电场中,粒子在介质中运动时会受到大小为f=kv粘滞阻力,y轴上P(0,0.08)点存在一个粒子源,能沿纸面向各个方向发射质量m=1.6×10-25kg、带电量q=+1.6×10-19C且进入介质中,观察到该粒子在介质中的径迹为直线(不计重力及粒子间下滑作用,粒子在介质中运动时电量不变).(1)求该粒子源发射粒子的速率;
(2)求k的值,并指出进入介质的其他粒子最终的运动情况(能给出相关参量的请给出参量的值);
(3)若撤去介质中的电场,求进入介质的粒子在介质中运动的轨迹长度l.
分析 (1)由题意知道粒子的运动过程是:在x轴上方做匀速圆周运动,在下方做直线运动,列出相应的式子就能求出粒子的速率.
(2)由平衡条件,在两个方向的合力为零,就能求出介质阻力常数.
(3)撤去电场后,粒子受阻力和洛仑兹力作用,运动情况非常复杂,从切向方向去考虑,用微元法来做,取一小段,在切向方向介质阻力使粒子的速度减小,变形之后,就是速度的变化与微元时间的积就是这一微元的位移,总的累加起来就是粒子运动的总长度.
解答  解:(1)由几何关系有 (R-0.08)2+0.162=R2
解:(1)由几何关系有 (R-0.08)2+0.162=R2
解得:R=0.2m
洛仑兹力提供向心力 $qvB=m\frac{{v}^{2}}{R}$
解得:v=8×103m/s
(2)设粒子进入介质的速度方向与x轴的夹角为θ,$sinθ=\frac{0.16}{0.2}=0.8$ θ=53°
如图,kv=qvb tan37°
k=4.8×10-21N•s/m
其他粒子在介质中最终做匀速直线运动
末速度大小都为 v=8×103m/s,方向与x轴正方向成53° 或:介质中其他粒子最
终都和上述粒子的速度大小、方向一样都做匀速直线运动.
(3)在切向应用牛顿第二定律有:
kv=mat
kv=m $\frac{△v}{△t}$ (在这里△v是速度大小的变化
k∑v△t=m∑△v,kl=mv-0
$l=\frac{mv}{k}=\frac{0.8}{3}m=0.27m$
答:(1)求该粒子源发射粒子的速率为8×103m/s.
(2)k的值是4.8×10-21N•s/m,进入介质的其他粒子最终的运动情况是做匀速直线运动.
(3)若撤去介质中的电场,进入介质的粒子在介质中运动的轨迹长度l为0.27m.
点评 本题的靓点在于第三问:撤去介质后粒子运动的长度,显然撤去介质后粒子的运动情况非常复杂,但在切向方向上粒子受到的合力就是介质的阻力,由牛顿第二定律写出表达式,但这里要注意的是把粒子的运动化为无数个微元,再把每一个微元切向位移累加就是粒子运动的总的路程.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案| A. | 电场和磁场同时用来提高粒子的动能 | |
| B. | 电场用来加速带电粒子,磁场只是用来改变带电粒子运行方向,使粒子回旋 | |
| C. | 粒子回旋的周期应与外加电场的周期一致 | |
| D. | 粒子获得的最大动能既与D形盒的半径有关,也与外加电场的电压有关 |
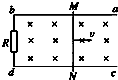 如图,两根相距为l的平行直导线ab、cd,b、d间连有一个固定电阻R,导轨电阻可忽略不计,MN为放在ab和cd上的一导体杆,与ab垂直,其电阻也为R.整个装置处于匀强磁场中,磁感应强度的大小为B,磁场方向垂直于导轨所在平面(指向图中纸面内).现对MN施力使它沿导轨方向以速度v做匀速运动.令U表示MN两端电压的大小,则( )
如图,两根相距为l的平行直导线ab、cd,b、d间连有一个固定电阻R,导轨电阻可忽略不计,MN为放在ab和cd上的一导体杆,与ab垂直,其电阻也为R.整个装置处于匀强磁场中,磁感应强度的大小为B,磁场方向垂直于导轨所在平面(指向图中纸面内).现对MN施力使它沿导轨方向以速度v做匀速运动.令U表示MN两端电压的大小,则( )| A. | U=$\frac{1}{2}vB$l | B. | U=$\frac{1}{3}$vBl | C. | U=vBl | D. | U=2vBl |
 如图(甲)所示,物体原来静止在水平地面上,用一水平力F拉物体,在F从0开始逐渐增大的过程中,物体先静止后又做变加速运动,其加速度a随外力F变化的图象如图(乙)所示.重力加速度g取10m/s2.根据题目提供的信息,下列判断正确的是( )
如图(甲)所示,物体原来静止在水平地面上,用一水平力F拉物体,在F从0开始逐渐增大的过程中,物体先静止后又做变加速运动,其加速度a随外力F变化的图象如图(乙)所示.重力加速度g取10m/s2.根据题目提供的信息,下列判断正确的是( )| A. | 物体的质量m=2kg | |
| B. | 物体与水平面间的动摩擦因数μ=0.3 | |
| C. | 物体与水平面的最大静摩擦力fmax=8N | |
| D. | 在F为10N时,物体的加速度a=2.5m/s2 |
| A. | 电场线越密的地方,电势越高 | |
| B. | 逆着电场线的方向电势逐渐升高 | |
| C. | 电势为零的地方,电场强度也一定为零 | |
| D. | 检验电荷沿等势面移动时,不受电场力的作用 |
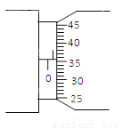
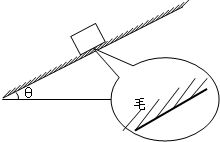 如图所示,一物体在蒙有动物毛皮的斜面上运动.由于毛皮表面的特殊性,引起物体的运动有如下特点:①顺着毛的生长方向运动时毛皮产生的阻力可以忽略;②逆着毛的生长方向运动会受到来自毛皮的滑动摩擦力,此时该物体与毛皮间的动摩擦因数μ=$\frac{\sqrt{3}}{4}$.已知斜面倾斜角为θ=30°.
如图所示,一物体在蒙有动物毛皮的斜面上运动.由于毛皮表面的特殊性,引起物体的运动有如下特点:①顺着毛的生长方向运动时毛皮产生的阻力可以忽略;②逆着毛的生长方向运动会受到来自毛皮的滑动摩擦力,此时该物体与毛皮间的动摩擦因数μ=$\frac{\sqrt{3}}{4}$.已知斜面倾斜角为θ=30°.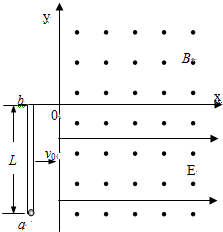 在一足够大的光滑水平面上建立如图所示的xoy坐标系,第一、四象限存在方向竖直向上、磁感应强度为B的匀强磁场;第四象限存在沿x轴正方向、电场强度为E的匀强电场.一长为L内壁光滑的薄玻璃管与y轴平行放置在水平面上的第三象限,开口端b与x轴重合,在玻璃管的a端放置一个直径比玻璃管直径略小的小球,小球带电荷量为-q、质量为m.玻璃管带着小球以水平速度v0沿x轴正方向运动,由于水平外力的作用,玻璃管进入磁场后速度保持不变,经一段时间后小球从玻璃管b端滑出并能在水平面内自由运动,最后从y轴飞离磁场.设运动过程中小球的电荷量保持不变,求:
在一足够大的光滑水平面上建立如图所示的xoy坐标系,第一、四象限存在方向竖直向上、磁感应强度为B的匀强磁场;第四象限存在沿x轴正方向、电场强度为E的匀强电场.一长为L内壁光滑的薄玻璃管与y轴平行放置在水平面上的第三象限,开口端b与x轴重合,在玻璃管的a端放置一个直径比玻璃管直径略小的小球,小球带电荷量为-q、质量为m.玻璃管带着小球以水平速度v0沿x轴正方向运动,由于水平外力的作用,玻璃管进入磁场后速度保持不变,经一段时间后小球从玻璃管b端滑出并能在水平面内自由运动,最后从y轴飞离磁场.设运动过程中小球的电荷量保持不变,求: 如图所示,理想变压器的原线圈与一矩形导轨相连,导轨间距l=10cm,导轨间有磁感应强度B=50$\sqrt{2}$T/s的匀强磁场,一金属杆紧贴导轨垂直放置.已知闭合铁芯上的三个线圈匝数n1=100匝,n2=50匝,n3=10匝,灯泡电阻RL1=10Ω,RL2=2Ω.现金属杆在外力的作用下以随时间变化规律为v=4cos100πt m/s的速度沿导轨做切割磁感线运动.请求出图中电压表和电流表的读数.
如图所示,理想变压器的原线圈与一矩形导轨相连,导轨间距l=10cm,导轨间有磁感应强度B=50$\sqrt{2}$T/s的匀强磁场,一金属杆紧贴导轨垂直放置.已知闭合铁芯上的三个线圈匝数n1=100匝,n2=50匝,n3=10匝,灯泡电阻RL1=10Ω,RL2=2Ω.现金属杆在外力的作用下以随时间变化规律为v=4cos100πt m/s的速度沿导轨做切割磁感线运动.请求出图中电压表和电流表的读数.