题目内容
14. 如图所示,一光滑宽阔的斜面固定在水平面上,其倾角为θ,高为h,现有一小球在A处以水平速度v0射出,最后从B处离开斜面,下面说法中正确的是( )
如图所示,一光滑宽阔的斜面固定在水平面上,其倾角为θ,高为h,现有一小球在A处以水平速度v0射出,最后从B处离开斜面,下面说法中正确的是( )| A. | 小球的运动轨迹为抛物线 | |
| B. | 小球到达B点的水平方向位移为$\frac{{v}_{0}\sqrt{\frac{2h}{g}}}{sinθ}$ | |
| C. | 小球到达点的时间为$\sqrt{\frac{2h}{g}}$ | |
| D. | 小球的加速度为gsinθ |
分析 小球做类平抛运动,根据沿斜面向下的位移求出运动的时间,抓住等时性求出水平方向的位移.
解答 解:A、小球所受的合力方向沿斜面向下,与初速度垂直,做类平抛运动,运动的轨迹为抛物线,故A正确.
B、根据牛顿第二定律得,小球的加速度a=$\frac{mgsinθ}{m}$=gsinθ,根据$\frac{h}{sinθ}=\frac{1}{2}a{t}^{2}$得,t=$\frac{1}{sinθ}\sqrt{\frac{2h}{g}}$,则水平方向的位移x=${v}_{0}t=\frac{{v}_{0}}{sinθ}\sqrt{\frac{2h}{g}}$,故B正确,C错误,D正确.
故选:ABD.
点评 解决本题的关键掌握处理类平抛运动的方法,结合等时性,根据牛顿第二定律和运动学公式进行求解.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
4. 如图所示,电源的电动势为E,内阻不计,A、B是两个不同的小灯泡,且RA<RB,L是一个自感系数很大、电阻不计的线圈.关于这个电路,以下说法正确的是( )
如图所示,电源的电动势为E,内阻不计,A、B是两个不同的小灯泡,且RA<RB,L是一个自感系数很大、电阻不计的线圈.关于这个电路,以下说法正确的是( )
 如图所示,电源的电动势为E,内阻不计,A、B是两个不同的小灯泡,且RA<RB,L是一个自感系数很大、电阻不计的线圈.关于这个电路,以下说法正确的是( )
如图所示,电源的电动势为E,内阻不计,A、B是两个不同的小灯泡,且RA<RB,L是一个自感系数很大、电阻不计的线圈.关于这个电路,以下说法正确的是( )| A. | 开关闭合瞬间,A、B同时亮 | |
| B. | 开关闭合瞬间,B先亮,A后亮 | |
| C. | 开关断开瞬间,A灯闪亮一下再逐渐熄灭 | |
| D. | 开关断开瞬间,电流向左通过A灯 |
5.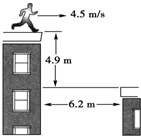 如图所示,一个电影替身演员准备跑过一个屋顶,然后水平跳跃并离开屋顶,在下一个建筑物的屋顶上着地.如果他在屋顶跑动的最大速度是4.5m/s,那么下列关于他能否安全跳过去的说法正确的是(g取9.8m/s2)( )
如图所示,一个电影替身演员准备跑过一个屋顶,然后水平跳跃并离开屋顶,在下一个建筑物的屋顶上着地.如果他在屋顶跑动的最大速度是4.5m/s,那么下列关于他能否安全跳过去的说法正确的是(g取9.8m/s2)( )
 如图所示,一个电影替身演员准备跑过一个屋顶,然后水平跳跃并离开屋顶,在下一个建筑物的屋顶上着地.如果他在屋顶跑动的最大速度是4.5m/s,那么下列关于他能否安全跳过去的说法正确的是(g取9.8m/s2)( )
如图所示,一个电影替身演员准备跑过一个屋顶,然后水平跳跃并离开屋顶,在下一个建筑物的屋顶上着地.如果他在屋顶跑动的最大速度是4.5m/s,那么下列关于他能否安全跳过去的说法正确的是(g取9.8m/s2)( )| A. | 他安全跳过去是可能的 | |
| B. | 他安全跳过去是不可能的 | |
| C. | 如果要安全跳过去,他在屋顶跑动的最小速度应大于6.2m/s | |
| D. | 如果要安全跳过去,他在屋顶跑动的最大速度应小于4.5m/s |
2. 如图所示,重10N的物体放在粗糙水平面上,用力F=8N的力斜向下推物体,F与水平面成30°角,物体与平面间的动摩擦因数μ=0.5,则:(设物体受到的最大静摩擦力等于滑动摩擦力)( )
如图所示,重10N的物体放在粗糙水平面上,用力F=8N的力斜向下推物体,F与水平面成30°角,物体与平面间的动摩擦因数μ=0.5,则:(设物体受到的最大静摩擦力等于滑动摩擦力)( )
 如图所示,重10N的物体放在粗糙水平面上,用力F=8N的力斜向下推物体,F与水平面成30°角,物体与平面间的动摩擦因数μ=0.5,则:(设物体受到的最大静摩擦力等于滑动摩擦力)( )
如图所示,重10N的物体放在粗糙水平面上,用力F=8N的力斜向下推物体,F与水平面成30°角,物体与平面间的动摩擦因数μ=0.5,则:(设物体受到的最大静摩擦力等于滑动摩擦力)( )| A. | 物体对地面的压力为14N | B. | 物体所受的摩擦力为7N | ||
| C. | 物体所受的合力为1N | D. | 物体所受的合力为零 |
3. 如图所示,在一端封闭的玻璃管中,用一段水银将管内气体与外界隔绝,管口向下放置,若将管倾斜,待稳定后则呈现的物理现象是( )
如图所示,在一端封闭的玻璃管中,用一段水银将管内气体与外界隔绝,管口向下放置,若将管倾斜,待稳定后则呈现的物理现象是( )
 如图所示,在一端封闭的玻璃管中,用一段水银将管内气体与外界隔绝,管口向下放置,若将管倾斜,待稳定后则呈现的物理现象是( )
如图所示,在一端封闭的玻璃管中,用一段水银将管内气体与外界隔绝,管口向下放置,若将管倾斜,待稳定后则呈现的物理现象是( )| A. | 封闭端内气体的压强增大 | B. | 封闭端内气体的压强减小 | ||
| C. | 封闭端内气体的压强不变 | D. | 封闭端内气体的体积减小 |
 如图所示,一个放置在水平台面上的木块,其质量为2kg,受到一个斜向下与水平方向成37°角的推力F=10N的作用,使木块从静止开始运动,5s后撤去推力,若木块与水平面间的动摩擦因数为0.1,则木块在水平面上运动的总位移为多少.(g取10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,一个放置在水平台面上的木块,其质量为2kg,受到一个斜向下与水平方向成37°角的推力F=10N的作用,使木块从静止开始运动,5s后撤去推力,若木块与水平面间的动摩擦因数为0.1,则木块在水平面上运动的总位移为多少.(g取10m/s2,sin37°=0.6,cos37°=0.8)
 如图所示,半径R=0.8m的四分之一光滑圆弧轨道位于竖直平面内,与长为S=2.0m的绝缘水平面CD平滑连接.水平面右侧空间存在互相垂直的匀强电场和匀强磁场,电场强度E=40N/C,方向竖直向上,磁场的磁感应强度B=1.0T,方向垂直纸面向外.两个质量均为m=2.0×10-6kg的小球a和b,a球不带电,b球带q=1.0×10-6C的正电,并静止于水平面右边缘处.将a球从圆弧轨道顶端由静止释放,运动到D点与b球发生正碰,碰撞时间极短,碰后两球粘合在一起飞入复合场中,最后落在地面上的P点.已知小球a在水平面上运动时所受的摩擦阻力f=0.1mg,PN=$\sqrt{3}$ND,取g=10m/s2.a、b均可作为质点.($\sqrt{3}$=1.73,结果保留三位有效数字)求:
如图所示,半径R=0.8m的四分之一光滑圆弧轨道位于竖直平面内,与长为S=2.0m的绝缘水平面CD平滑连接.水平面右侧空间存在互相垂直的匀强电场和匀强磁场,电场强度E=40N/C,方向竖直向上,磁场的磁感应强度B=1.0T,方向垂直纸面向外.两个质量均为m=2.0×10-6kg的小球a和b,a球不带电,b球带q=1.0×10-6C的正电,并静止于水平面右边缘处.将a球从圆弧轨道顶端由静止释放,运动到D点与b球发生正碰,碰撞时间极短,碰后两球粘合在一起飞入复合场中,最后落在地面上的P点.已知小球a在水平面上运动时所受的摩擦阻力f=0.1mg,PN=$\sqrt{3}$ND,取g=10m/s2.a、b均可作为质点.($\sqrt{3}$=1.73,结果保留三位有效数字)求: 如图所示,边长为7cm的正方形OABC区域内存在B=0.1T,方向垂直纸面向外的匀强磁场,在此正方形区域内有一点P,P点到OC边和BC边的距离均为1cm,在P点有一个发射正离子的装置,能够连续不断地向纸面内的各个方向发射出速率不同的正离子,离子的质量m=1.0×10-14kg,电荷量q=1.0×10-5C,离子的重力不计,不考虑离子间的相互作用力.(计算结果保留两位有效数字)求:
如图所示,边长为7cm的正方形OABC区域内存在B=0.1T,方向垂直纸面向外的匀强磁场,在此正方形区域内有一点P,P点到OC边和BC边的距离均为1cm,在P点有一个发射正离子的装置,能够连续不断地向纸面内的各个方向发射出速率不同的正离子,离子的质量m=1.0×10-14kg,电荷量q=1.0×10-5C,离子的重力不计,不考虑离子间的相互作用力.(计算结果保留两位有效数字)求: