Question

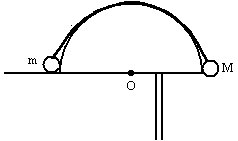
如图所示，两物体的质量分别为M和m(M＞m)，用细绳连接后跨在半径为R的固定光滑半圆柱体上，两物体刚好位于其水平直径的两端，释放后它们由静止开始运动，求m到达圆柱顶端时对圆柱顶端的压力．

Answer 1

答案：
解析：

对m和M及地球组成的系统，圆柱面对m的弹力不做功，只有重力对系统做功，系统的机械能守恒，据此可求出m运动到圆柱顶时的速度，从而可知道它在最高点时的向心加速度，由牛顿第二定律即可求出m受到的支持力． 　　取m，M的起始位置为重力势能零点，则系统初始位置的机械能E1＝0． 设当m运动到圆柱顶时的速度为v，此时M向下移动，则该状态系统的机械能 　　　　　　   E2＝mgR＋(－Mg·)＋(M＋m)v2． 由机械能守恒有E1＝E2，即 　　　　　　　　 0＝mgR－Mg·＋(M＋m)v2． 由此解得 　　　　　　　　　　 v2＝． 设m在圆柱顶时所受的支持力为N，由牛顿第二定律有 　　　　　　　　　　   mg－N＝m． 所以 　　　　　　　　   N＝mg－m＝mg·． 根据牛顿第三定律，m对圆柱顶端的压力大小等于N．即 　　　　　　　　　　  ＝mg·．

提示：

对m和M组成的系统，内力做功代数和为零，因此系统机械能守恒．注意m上升的高度和M下降高度的不同，两者的速度都沿绳的方向，两者速度大小相等．