题目内容
2.如图甲所示为“离心轨道演示仪”,由倾斜曲面轨道和半径R=0.2m的圆轨道平滑连接而成.现将其竖直固定在一水平桌面上(如图乙所示),其圆形轨道部分与桌面相切于A点,桌面离地距离h1=0.8m.现从曲面轨道某处静止释放一质量m=0.1kg的小滑块,不计滑块与轨道各处的摩擦,取g=10m/s2.(1)若滑块从A处刚进入圆轨道时,它对轨道的压力大小力FNA=10mg,求:滑块开始释放处离桌面的高度h和滑块运动到圆弧轨道最高点B处时对轨道的压力大小FNB;
(2)己知A点与桌面右边缘C点的距离为0.5m,桌面右侧d1=0.6m处有一直径d2=0.6m、高h2=0.35m的开口向上的圆桶,滑块与桌面间的动摩擦因素μ=0.8.滑块从曲面轨道某处静止释放后,沿圆形轨道运动一周后从A点离开,并在桌面上继续向右运动直至落入圆桶中,则滑块释放处离桌面至少多高?

分析 (1)由牛顿第三定律求得在A点受到的支持力,然后由牛顿第二定律求得在A点的速度,即可由机械能守恒求得h和在B的速度,然后对滑块在B点应用牛顿第二定律求得支持力,即可由牛顿第三定律求得压力;
(2)根据滑块落入桶中,由平抛运动规律求得在C的速度范围,然后对滑块从静止到C应用动能定理即可求得高度范围,再对滑块在B点应用牛顿第二定律求得速度范围,然后由机械能守恒求得高度范围,两个高度范围的共值即可能实际能取的高度范围,即可得到最小高度.
解答 解:(1)滑块从A处刚进入圆轨道时,它对轨道的压力大小力FNA=10mg,那么由牛顿第三定律可知:滑块受到的支持力也为10mg,对滑块应用牛顿第二定律可得:$10mg-mg=\frac{m{{v}_{A}}^{2}}{R}$;
滑块运动过程中只有重力做功,故机械能守恒,则有:$mgh=\frac{1}{2}m{{v}_{A}}^{2}=\frac{9}{2}mgR$,$\frac{1}{2}m{{v}_{A}}^{2}=2mgR+\frac{1}{2}m{{v}_{B}}^{2}$;
所以,$h=\frac{9}{2}R=0.9m$,${v}_{B}=\sqrt{5gR}$,那么,对滑块在B点应用牛顿第二定律可得:滑块受到的支持力4N,故由牛顿第三定律可得:滑块运动到圆弧轨道最高点B处时对轨道的压力大小为4N;
(2)滑块从C到圆桶做平抛运动,故有:${h}_{1}-{h}_{2}=\frac{1}{2}g{t}^{2}$,d1≤vCt≤d1+d2,所以,t=0.3s,2m/s≤vC≤4m/s;
滑块要能通过B点,那么在B点应用牛顿第二定律可得:$mg≤\frac{m{v}_{B}{′}^{2}}{R}$;
对滑块从静止到B应用动能定理可得:$mg(h-2R)=\frac{1}{2}m{v}_{B}{′}^{2}≥\frac{1}{2}mgR$,所以,$h≥\frac{5}{2}R=0.5m$;
对滑块从静止到C应用动能定理可得:$mgh-μmgAC=\frac{1}{2}m{{v}_{C}}^{2}$,所以,0.6m≤h≤1.2m;
所以,滑块释放处离桌面至少0.6m;
答:(1)若滑块从A处刚进入圆轨道时,它对轨道的压力大小力FNA=10mg,则滑块开始释放处离桌面的高度h为0.9m,滑块运动到圆弧轨道最高点B处时对轨道的压力大小FNB为4N;
(2)己知A点与桌面右边缘C点的距离为0.5m,桌面右侧d1=0.6m处有一直径d2=0.6m、高h2=0.35m的开口向上的圆桶,滑块与桌面间的动摩擦因素μ=0.8.滑块从曲面轨道某处静止释放后,沿圆形轨道运动一周后从A点离开,并在桌面上继续向右运动直至落入圆桶中,则滑块释放处离桌面至少0.6m.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.

| A. | 合运动的速度一定比分运动的速度大 | |
| B. | 合运动的速度一定比分运动的速度小 | |
| C. | 合运动的速度可能比分运动的速度小 | |
| D. | 两个匀速直线运动的合运动可能是曲线运动 |
 某质量为1500kg的汽车以30m/s的速度匀速直线行驶,由于要礼让行人穿过马路,司机在t=0时开始刹车,t=10s时关闭油门,汽车最终恰好停在斑马线外,其速度随时间的变化关系如图所示,下列判断正确的是( )
某质量为1500kg的汽车以30m/s的速度匀速直线行驶,由于要礼让行人穿过马路,司机在t=0时开始刹车,t=10s时关闭油门,汽车最终恰好停在斑马线外,其速度随时间的变化关系如图所示,下列判断正确的是( )| A. | 0~10s内,汽车做加速度减小的减速运动 | |
| B. | 0~10s内,汽车所受合力做的功为6×106J | |
| C. | 0~10s内,汽车所受合力做功的平均功率约为6.56×104W | |
| D. | 10s~15s内,汽车所受的阻力大小为1500N |
| A. | 红外线传感器 | B. | 气体传感器 | C. | 温度传感器 | D. | 声音传感器 |
| A. | 路程为8m | B. | 位移的大小为32m | C. | 位移的大小为8m | D. | 位移的方向向东 |

 如图所示,质量为m的物体从高为h,倾角为θ的斜面顶端由静止开始沿斜面下滑,最后停在水平面上,已知物体与斜面、水平面间的动摩擦因数为μ,斜面与平面交接处通过小圆弧平滑连接.求:
如图所示,质量为m的物体从高为h,倾角为θ的斜面顶端由静止开始沿斜面下滑,最后停在水平面上,已知物体与斜面、水平面间的动摩擦因数为μ,斜面与平面交接处通过小圆弧平滑连接.求: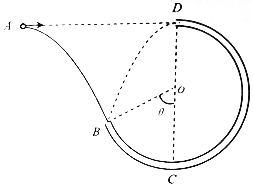 如图所示,一个可视为质点的质量为m=1kg的小球,以某一初速度从A点水平抛出,恰好从竖直圆管BCD的B点沿切线方向进入圆管,经BCD后从圆管的最高点D水平射出,恰好又落到B点.已知圆弧的半径为R=0.3m,且A与D在同一水平线上,BC弧对应的圆心角θ=60°,不计空气阻力,g=10m/s2.求:
如图所示,一个可视为质点的质量为m=1kg的小球,以某一初速度从A点水平抛出,恰好从竖直圆管BCD的B点沿切线方向进入圆管,经BCD后从圆管的最高点D水平射出,恰好又落到B点.已知圆弧的半径为R=0.3m,且A与D在同一水平线上,BC弧对应的圆心角θ=60°,不计空气阻力,g=10m/s2.求: