题目内容
3. 如图所示,ABCDMNC′PQ为竖直轨道.其中,CDMNC′是圆心为O、半径为R=0.1m的圆轨道.BC和C′P都是半径为2R的圆弧轨道,圆心为M点.MOC(C′)在同一竖直线上.直轨道AB和PQ分别相切与圆弧轨道的B、P两点,直轨道与水平方向的夹角均为37°.PQ是动摩擦因数为μ=0.5的粗糙轨道,其余轨道均光滑.现将质量m=0.2kg的小滑块(可视为质点)从距离B点L=4m的A处静止释放.求:(已知sin37°=0.6,cos37°=0.8,g取10m/s2)
如图所示,ABCDMNC′PQ为竖直轨道.其中,CDMNC′是圆心为O、半径为R=0.1m的圆轨道.BC和C′P都是半径为2R的圆弧轨道,圆心为M点.MOC(C′)在同一竖直线上.直轨道AB和PQ分别相切与圆弧轨道的B、P两点,直轨道与水平方向的夹角均为37°.PQ是动摩擦因数为μ=0.5的粗糙轨道,其余轨道均光滑.现将质量m=0.2kg的小滑块(可视为质点)从距离B点L=4m的A处静止释放.求:(已知sin37°=0.6,cos37°=0.8,g取10m/s2)(1)小滑块在AB轨道上运动时的加速度大小;
(2)小滑块第一次经过M点时,轨道对它的作用力大小;
(3)小滑块能通过M点的次数.
分析 1、根据牛顿第二定律求解小滑块在AB轨道上运动时的加速度大小
2、根据动能定理研究A点到M点,在M点,根据牛顿第二定律求解
3、小滑块恰好经过最高点M时,根据牛顿第二定律求解M点速度,根据动能定理多次选择不同研究过程求解.
解答 解:(1)小滑块在AB轨道上运动时受重力和支持力,
根据牛顿第二定律得mgsinθ=ma
a=gsinθ=6m/s2
(2)根据动能定理研究A点到M点,
$mg(Lsin{37^o}-2Rcos{37^o})=\frac{1}{2}m{v^2}$
在M点,根据牛顿第二定律得$mg+{F_N}=m\frac{v^2}{R}$
解得:FN=87.6N
(3)小滑块恰好经过最高点M时,根据牛顿第二定律得:$mg=m\frac{v_M^2}{R}$
vM=1m/s
小滑块能过最高点,根据动能定理得
$2mgRcos{37^o}=\frac{1}{2}mv_P^2-\frac{1}{2}mv_M^2$
${v_P}=\sqrt{4.2}m/s$
设小物块第一次在PQ轨道上速度减到0离P点的高点为h1,有
$mg(Lsin{37^o}-{h_1})-μmg\frac{h_1}{tanθ}=0$
h1=1.44m
设小物块从第一次的最高点运动的P的速度为v1,有$mg{h_1}-μmg\frac{h_1}{tanθ}=\frac{1}{2}mv_1^2$
${v_1}=\sqrt{9.6}m/s$
设小物块第二次在PQ轨道上速度减到0离P点的高点为h2,有$-mg{h_2}-μmg\frac{h_2}{tanθ}=0-\frac{1}{2}mv_1^2$
h2=0.288m设小物块从第二次的最高点运动的P的速度为v2,有$mg{h_2}-μmg\frac{h_2}{tanθ}=\frac{1}{2}mv_2^2$
${v_1}=\sqrt{1.92}m/s<\sqrt{4.2}m/s$不能过最高点.
小滑块能通过M点3次
答:(1)小滑块在AB轨道上运动时的加速度大小是6m/s2;
(2)小滑块第一次经过M点时,轨道对它的作用力大小是87.6N;
(3)小滑块能通过M点3次
点评 解决本题的关键理清物块的运动过程,结合动能定理进行求解,本题对数学能力的要求较高,知道物块不能到达M点的条件,结合数学知识进行求解.

| A. | 若物体的运动状态发生改变,则它一定做曲线运动 | |
| B. | 若物体做曲线运动,则它的运动状态一定改变 | |
| C. | 竖直平面内做匀速圆周运动的物体,其合外力可能不指向圆心 | |
| D. | 匀速直线运动和初速度为零的匀加速直线运动的合运动一定是曲线运动 |
 如图所示,电池组、滑动变阻器、带铁芯的线圈A、线圈B、电流计(零刻线在正中位置)及开关S1、S2如图所示连接在一起,在开关S1、S2闭合、线圈A在线圈B中.某同学发现当他将滑动变阻器的滑动片P向左滑动时,电流计指针向右偏转,由此可以推断:将线圈A从线圈B中突然拔出时,电流表指针将左偏;当开关S1突然断开时,电流表指针将左偏;当开关S2突然断开时,电流表指针将不偏(填“左偏”、“右偏”、“不偏”).
如图所示,电池组、滑动变阻器、带铁芯的线圈A、线圈B、电流计(零刻线在正中位置)及开关S1、S2如图所示连接在一起,在开关S1、S2闭合、线圈A在线圈B中.某同学发现当他将滑动变阻器的滑动片P向左滑动时,电流计指针向右偏转,由此可以推断:将线圈A从线圈B中突然拔出时,电流表指针将左偏;当开关S1突然断开时,电流表指针将左偏;当开关S2突然断开时,电流表指针将不偏(填“左偏”、“右偏”、“不偏”). 质量m=3kg的质点静止在光滑水平面上的直角坐标系的原点O(坐标系所在平面即为水平面),先用沿+x轴方向的力F1=9N作用了2s,然后撤去F1;再用沿+y轴方向的力F2=24N作用了1s,请列出必要的表达式,计算出质点在3s末的位置坐标并在图中画出质点在这3s内的质点的运动轨迹.
质量m=3kg的质点静止在光滑水平面上的直角坐标系的原点O(坐标系所在平面即为水平面),先用沿+x轴方向的力F1=9N作用了2s,然后撤去F1;再用沿+y轴方向的力F2=24N作用了1s,请列出必要的表达式,计算出质点在3s末的位置坐标并在图中画出质点在这3s内的质点的运动轨迹.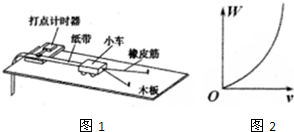 某实验小组采用如图1所示的装置探究功与速度变化的关系,小车在橡皮筋的作用下弹出后,沿木板滑行.打点计时器的工作频率为50Hz.
某实验小组采用如图1所示的装置探究功与速度变化的关系,小车在橡皮筋的作用下弹出后,沿木板滑行.打点计时器的工作频率为50Hz. 如图所示,一质量为m1的小物块从平台A点以v0=5m/s的速度水平抛出落到C点,且恰好从C点沿切线方向进入光滑圆弧轨道CD到达D点,再滑上传送带DE.已知AB高度h1=5m,CD竖直高度h2=5m,D点切线水平并与传送带DE平滑连接,传送带以速度V=5m/s沿顺时针方向转动,小物块m1与传送带间的动摩擦因数为μ1=0.5,g=10m/s2.求:
如图所示,一质量为m1的小物块从平台A点以v0=5m/s的速度水平抛出落到C点,且恰好从C点沿切线方向进入光滑圆弧轨道CD到达D点,再滑上传送带DE.已知AB高度h1=5m,CD竖直高度h2=5m,D点切线水平并与传送带DE平滑连接,传送带以速度V=5m/s沿顺时针方向转动,小物块m1与传送带间的动摩擦因数为μ1=0.5,g=10m/s2.求: 如图所示为某种透明材料制成的一块柱体形棱镜的水平截面图,其中FD为四分之一圆弧,圆心为O,光束从AB面入射,入射角θ1,它射入棱镜后射在BF面上的O点并恰好不从BF面射出,光路如图,图中∠C=53°.(已知sin53°=0.8,cos53°=0.6).求:
如图所示为某种透明材料制成的一块柱体形棱镜的水平截面图,其中FD为四分之一圆弧,圆心为O,光束从AB面入射,入射角θ1,它射入棱镜后射在BF面上的O点并恰好不从BF面射出,光路如图,图中∠C=53°.(已知sin53°=0.8,cos53°=0.6).求: