题目内容
6. 质量均匀分布的导电正方形线框abcd总质量为m,边长为l,每边的电阻均为r0.线框置于xoy光滑水平面上,处在磁感应强度大小为B的匀强磁场中.如图,现将ab通过柔软轻质导线接到电压为U的电源两端(电源内阻不计,导线足够长),下列说法正确的是( )
质量均匀分布的导电正方形线框abcd总质量为m,边长为l,每边的电阻均为r0.线框置于xoy光滑水平面上,处在磁感应强度大小为B的匀强磁场中.如图,现将ab通过柔软轻质导线接到电压为U的电源两端(电源内阻不计,导线足够长),下列说法正确的是( )| A. | 若磁场方向竖直向下,则线框的加速度大小为$\frac{4BlU}{3m{r}_{0}}$ | |
| B. | 若磁场方向沿x轴正方向,则线框保持静止 | |
| C. | 若磁场方向沿y轴正方向,发现线框以cd边为轴转动,则$U>\frac{mg{r}_{0}}{2Bl}$ | |
| D. | 若磁场方向沿y轴正方向,线框以cd边为轴转动且cd边未离开水平面,则线框转动过程中的最大动能为$\frac{B{l}^{2}U}{{r}_{0}}-\frac{mgl}{2}$ |
分析 根据左手定则可知,安培力的方向;由闭合电路欧姆定律与安培力的公式,即可求解加速度;根据通电导线的受力与重力相比,利用动能定理即可判断出.
解答 解:A、根据左手定则,安培力的方向沿+y轴方向
${I}_{ab}=\frac{U}{{r}_{0}}$,
${I}_{dc}=\frac{U}{3{r}_{0}}$
根据F=BIl,线框所受的安培力的合力为:F=Fab+Fdc=$Bl(\frac{U}{{r}_{0}}+\frac{U}{3{r}_{0}})$
线框的加速度大小为:$a=\frac{F}{m}$=$\frac{4BlU}{3m{r}_{0}}$,故A正确;
B、若磁场方向沿x轴正方向,ad边受到的安培力竖直向下,cd边受到的安培力竖直向上,故线框不可能处于静止,故B错误;
C、若磁场方向沿y轴正方向,发现线框以cd边为轴转动,则,根据动能定理可得$\frac{BLU}{{r}_{0}}•L-mg•\frac{1}{2}L>0$,解得:$U>\frac{mg{r}_{0}}{2Bl}$,故C正确;
D、在转动过程中,由于ab边的安培力大于线框的重力,故在安培力作用下,线框的动能一直增大,故有:${E}_{k}=\frac{BLU}{{r}_{0}}•L-mg•\frac{L}{2}$=$\frac{B{l}^{2}U}{{r}_{0}}-\frac{mgl}{2}$,故D正确
故选:ACD
点评 考查左手定则的理解,知道与右手定则区别,掌握闭合电路欧姆定律,学会由力来判定运动情况,利用动能定理判断最大动能

练习册系列答案
相关题目
20.一辆质量为5t的汽车,以恒定的速率v=20m/s通过拱桥,拱桥的半径r=50m,重力加速度g=10m/s2,则在最高点时汽车对桥的压力为( )
| A. | 104N | B. | 3*104N | C. | 5*104N | D. | 7*104N |
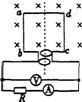
17. 在一个闭合铁芯上绕两个彼此绝缘的线圈A和B,线圈A的两端与处于匀强磁场中的两平行金属导轨上放一金属导体棒ab,线圈B与一电容器C相接,如图所示,若要使电容器C的上极板带正电,则导体棒ab(导轨电阻不计)的运动情况可能是( )
在一个闭合铁芯上绕两个彼此绝缘的线圈A和B,线圈A的两端与处于匀强磁场中的两平行金属导轨上放一金属导体棒ab,线圈B与一电容器C相接,如图所示,若要使电容器C的上极板带正电,则导体棒ab(导轨电阻不计)的运动情况可能是( )
 在一个闭合铁芯上绕两个彼此绝缘的线圈A和B,线圈A的两端与处于匀强磁场中的两平行金属导轨上放一金属导体棒ab,线圈B与一电容器C相接,如图所示,若要使电容器C的上极板带正电,则导体棒ab(导轨电阻不计)的运动情况可能是( )
在一个闭合铁芯上绕两个彼此绝缘的线圈A和B,线圈A的两端与处于匀强磁场中的两平行金属导轨上放一金属导体棒ab,线圈B与一电容器C相接,如图所示,若要使电容器C的上极板带正电,则导体棒ab(导轨电阻不计)的运动情况可能是( )| A. | 沿轨道向右做匀速运动 | B. | 沿轨道向左做加速运动 | ||
| C. | 沿轨道向右做减速运动 | D. | 沿轨道向左做减速运动 |
11. 在竖直直角坐标系xOy平面内有一四分之一光滑圆柱体的截面OAB,半径为R.在x轴上的P点斜向左上方抛出一个小球(可视为质点).小球的运动轨迹与圆柱体相切于D点,且到达y轴上的C点时速度与y轴垂直,OD与OB的夹角为60°,不计空气阻力,重力加速度大小为g.则小球在P点的速度大小为( )
在竖直直角坐标系xOy平面内有一四分之一光滑圆柱体的截面OAB,半径为R.在x轴上的P点斜向左上方抛出一个小球(可视为质点).小球的运动轨迹与圆柱体相切于D点,且到达y轴上的C点时速度与y轴垂直,OD与OB的夹角为60°,不计空气阻力,重力加速度大小为g.则小球在P点的速度大小为( )
 在竖直直角坐标系xOy平面内有一四分之一光滑圆柱体的截面OAB,半径为R.在x轴上的P点斜向左上方抛出一个小球(可视为质点).小球的运动轨迹与圆柱体相切于D点,且到达y轴上的C点时速度与y轴垂直,OD与OB的夹角为60°,不计空气阻力,重力加速度大小为g.则小球在P点的速度大小为( )
在竖直直角坐标系xOy平面内有一四分之一光滑圆柱体的截面OAB,半径为R.在x轴上的P点斜向左上方抛出一个小球(可视为质点).小球的运动轨迹与圆柱体相切于D点,且到达y轴上的C点时速度与y轴垂直,OD与OB的夹角为60°,不计空气阻力,重力加速度大小为g.则小球在P点的速度大小为( )| A. | $\sqrt{5Rg}$ | B. | 2$\sqrt{Rg}$ | C. | $\sqrt{3Rg}$ | D. | $\sqrt{2Rg}$ |
16.关于重力势能,下列说法中正确的是( )
| A. | 物体的位置一旦确定,它的重力势能的大小也随之确定 | |
| B. | 物体与零势面的距离越大,它的重力势能也越大 | |
| C. | 一个物体的重力势能从-5J变化到-3J,重力势能变大了 | |
| D. | 在地面上的物体,它具有的重力势能不一定等于零 |
 如图所示,如果线圈abcd的面积是$\frac{11\sqrt{2}}{50}$m2,共100匝,线圈电阻为2Ω,外接电阻R=9Ω,匀强磁场的磁感应强度B=$\frac{1}{π}$T,当线圈以300r/min的转速绕垂直于磁场的轴匀速转动时.求:
如图所示,如果线圈abcd的面积是$\frac{11\sqrt{2}}{50}$m2,共100匝,线圈电阻为2Ω,外接电阻R=9Ω,匀强磁场的磁感应强度B=$\frac{1}{π}$T,当线圈以300r/min的转速绕垂直于磁场的轴匀速转动时.求:

