题目内容
12.如果有一星球的密度跟地球的密度相同,又已知它表面的重力加速度是地球表面重力加速度的2倍,则该星球质量与地球质量之比是( )?| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{8}$ | D. | 8 |
分析 根据万有引力等于重力,列出等式表示出重力加速度.根据密度与质量关系代入表达式找出与星球半径的关系,再求出质量关系.
解答 解:根据万有引力等于重力,列出等式:$\frac{GMm}{{R}^{2}}$=mg,
得:g=$\frac{GM}{{R}^{2}}$,其中M是任一星球的质量,r应该是物体在某位置到星球球心的距离.
根据密度与质量关系得:M=ρ•$\frac{4}{3}$πR3,
则得:g=ρ•$\frac{4}{3}$πR,
星球的密度跟地球密度相同,星球的表面重力加速度是地球表面重力加速度的2倍,所以星球的半径也是地球的2倍,
所以再根据M=ρ•$\frac{4}{3}$πR3,得:星球质量是地球质量的8倍.
故选:D.
点评 求一个物理量之比,我们应该把这个物理量先用已知的物理量表示出来,再根据表达式进行比较.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.从距地面高h处水平抛出一小石子,石子在空中飞行过程中(空气阻力不计),下列说法不正确的是( )
| A. | 石子的运动为匀变速运动 | |
| B. | 石子抛出时速度越大,石子在空中飞行时间越长 | |
| C. | 石子每秒内速度的变化量恒定不变 | |
| D. | 石子在任何时刻的速度与其竖直分速度之差为一恒量 |
3.水的摩尔质量为18g/mol,密度为1g/cm3,则每个水分子的质量为2.99×10-26kg,每个水分子所占体积为2.99×10-29m3.(${N}_{A}=6.02×1{0}^{23}$个)
1.对于质量一定的物体,下列说法中正确的是( )
| A. | 物体的动能不变,则其速度一定也不变 | |
| B. | 物体的速度不变,则其动能一定也不变 | |
| C. | 物体的动能不变,说明物体的运动状态没有改变 | |
| D. | 物体的动能不变,说明物体所受的合外力一定为零 |
 如图所示,一定质量的理想气体从状态A变化到状态B,再由状态B变化到状态C.已知状态A的温度为300K.
如图所示,一定质量的理想气体从状态A变化到状态B,再由状态B变化到状态C.已知状态A的温度为300K. 如图所示,质量为1.0×103kg的汽车,行驶到一座半径为40m的圆形凸桥顶时,假如汽车对桥的压力恰好为零.(g取10m/s2)
如图所示,质量为1.0×103kg的汽车,行驶到一座半径为40m的圆形凸桥顶时,假如汽车对桥的压力恰好为零.(g取10m/s2)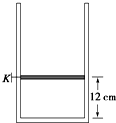 如图所示,足够长的圆柱形气缸竖直放置,其横截面积为1×10-3m2,气缸内有质量m=1kg的活塞,活塞与气缸壁封闭良好,不计摩擦.开始时活塞被销子K销于如图位置,离缸底12cm,此时气缸内被封闭气体的压强1.5×105Pa,温度为300K.外界大气压为1.0×105Pa,g=10m/s2.
如图所示,足够长的圆柱形气缸竖直放置,其横截面积为1×10-3m2,气缸内有质量m=1kg的活塞,活塞与气缸壁封闭良好,不计摩擦.开始时活塞被销子K销于如图位置,离缸底12cm,此时气缸内被封闭气体的压强1.5×105Pa,温度为300K.外界大气压为1.0×105Pa,g=10m/s2.