题目内容
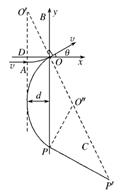
如图所示,在坐标系xOy中,过原点的直线OC与x轴正向的夹角φ=120°,在OC右侧有一匀强电场;在第二、三象限内有一匀强磁场,其上边界与电场边界重叠、右边界为y轴、左边界为图中平行于y轴的虚线,磁场在磁感应强度大小为B,方向垂直纸面向里.一带正电荷q、质量为m的粒子以某一速度自磁场左边界上的A点射入磁场区域,并从O点射出,粒子射出磁场的速度方向与x轴的夹角θ=30°,大小为v.粒子在磁场中的运动轨迹为纸面内的一段圆弧,且弧的半径为磁场左右边界间距的两倍.粒子进入电场后,在电场力的作用下又由O点返回磁场区域,经过一段时间后再次离开磁场.已知粒子从A点射入到第二次离开磁场所用的时间恰好等于粒子在磁场中做圆周运动的周期.忽略重力的影响.求
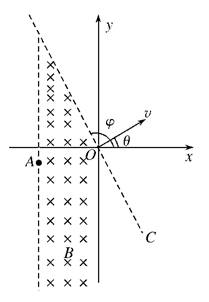
(1)粒子经过A点时速度的方向和A点到x轴的距离;
(2)匀强电场的大小和方向;
(3)粒子从第二次离开磁场到再次进入电场时所用的时间.
(1)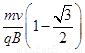 (2)
(2)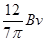 ,与x轴正向夹角为150° (3)
,与x轴正向夹角为150° (3)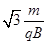
【解析】(1)设磁场左边界与x轴相交于D点,与CO相交于O′点,由几何关系可知,直线OO′与粒子过O点的速度v垂直.在直角三角形OO′D中∠OO′D=30°.设磁场左右边界间距为d,则OO′=2d.依题可知,粒子第一次进入磁场的运动轨迹的圆心即为O′点,圆弧轨迹所对的圆心角为30°,且O′A为圆弧的半径R.由此可知,粒子自A点射入磁场的速度与左边界垂直.A点到
x轴的距离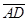 =R(1-cos30°) ①
=R(1-cos30°) ①
由洛伦兹力公式、牛顿第二定律及圆周运动的规律,得qvB=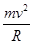 ②
②
联立①②式得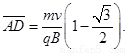 ③
③
(2)设粒子在磁场中做圆周运动的周期为T,第一次在磁场中飞行的时间为t1,有
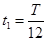 ④
④
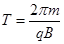 ⑤
⑤
依题意,匀强电场的方向与x轴正向夹角应为150°.由几何关系可知,粒子再次从O点进入磁场的速度方向与磁场右边界夹角为60°.设粒子第二次在磁场中飞行的圆弧的圆心为O″,O″必定在直线OC上.设粒子射出磁场时与磁场右边界交于P点,则∠OO″P=120°.
设粒子第二次进入磁场在磁场中运动的时间为t2,有
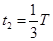 ⑥
⑥
设带电粒子在电场中运动的时间为t3,依题意得
t3=T-(t1+t2) ⑦
由匀变速运动的规律和牛顿定律可知,-v=v-at3 ⑧
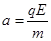 ⑨
⑨
联立④⑤⑥⑦⑧⑨可得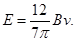 ⑩
⑩
(3)粒子自P点射出后将沿直线运动.设其由P′点再次进入电场,由几何关系知
∠O″P′P=30°?B11?
三角形OPP
′为等腰三角形.设粒子在P、P′两点间运动的时间为t4,有 (12)
(12)
又由几何关系知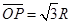 ? (13)
? (13)
联立②(12)(13)式得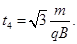

 (2011?福建模拟)如图所示,在坐标系xOy中,x<0的区域空间存在着垂直纸面向外的匀强磁场,x>0的区域空间存在着电场强度大小E=
(2011?福建模拟)如图所示,在坐标系xOy中,x<0的区域空间存在着垂直纸面向外的匀强磁场,x>0的区域空间存在着电场强度大小E=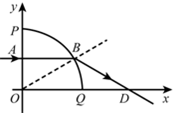 [物理--选修3-4]
[物理--选修3-4] (2011?武汉模拟)如图所示,在坐标系xOy内有一半径为a的圆形区域,圆心坐标为O1(a,0),圆内分布有垂直纸面向里的匀强磁场.在直线y=a的上方和直线x=2a的左侧区域内,有一沿y轴负方向的匀强电场,场强大小为E.一质量为m、电荷量为+q(q>0)的粒子以速度v从O点垂直于磁场方向射入,当速度方向沿x轴正方向时,粒子恰好从O1点正上方的A点射出磁场,不计粒子重力.
(2011?武汉模拟)如图所示,在坐标系xOy内有一半径为a的圆形区域,圆心坐标为O1(a,0),圆内分布有垂直纸面向里的匀强磁场.在直线y=a的上方和直线x=2a的左侧区域内,有一沿y轴负方向的匀强电场,场强大小为E.一质量为m、电荷量为+q(q>0)的粒子以速度v从O点垂直于磁场方向射入,当速度方向沿x轴正方向时,粒子恰好从O1点正上方的A点射出磁场,不计粒子重力.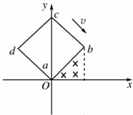 如图所示,在坐标系xOy中,有边长为L的正方形金属线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧的Ⅰ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合,下边界与x轴重合,右边界与y轴平行.t=0时刻,线圈以恒定的速度v沿垂直于磁场上边界的方向穿过磁场区域.取a→b→c→d→a的感应电流方向为正,则在线圈穿越磁场区域的过程中,感应电流i、ab间的电势差Uab随时间t变化的图线是下图中的( )
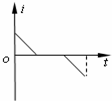
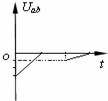
如图所示,在坐标系xOy中,有边长为L的正方形金属线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧的Ⅰ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合,下边界与x轴重合,右边界与y轴平行.t=0时刻,线圈以恒定的速度v沿垂直于磁场上边界的方向穿过磁场区域.取a→b→c→d→a的感应电流方向为正,则在线圈穿越磁场区域的过程中,感应电流i、ab间的电势差Uab随时间t变化的图线是下图中的( )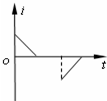

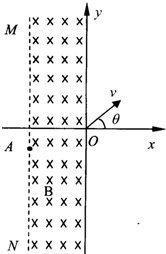 如图所示,在坐标系xOy中,y轴右侧有一匀强电场;在第二、三象限内有一有界匀强磁场,其上、下边界无限远,右边界为y轴、左边界为平行于y轴的虚线,磁场的磁感应强度大小为B,方向垂直纸面向里.一带正电,电量为q、质量为m的粒子以某一速度自磁场左边界上的A点射入磁场区域,并从O点射出,粒子射出磁场的速度方向与x轴的夹角θ=45°,大小为v.粒子在磁场中的运动轨迹为纸面内的一段圆弧,且弧的半径为磁场左右边界间距的
如图所示,在坐标系xOy中,y轴右侧有一匀强电场;在第二、三象限内有一有界匀强磁场,其上、下边界无限远,右边界为y轴、左边界为平行于y轴的虚线,磁场的磁感应强度大小为B,方向垂直纸面向里.一带正电,电量为q、质量为m的粒子以某一速度自磁场左边界上的A点射入磁场区域,并从O点射出,粒子射出磁场的速度方向与x轴的夹角θ=45°,大小为v.粒子在磁场中的运动轨迹为纸面内的一段圆弧,且弧的半径为磁场左右边界间距的