题目内容
19.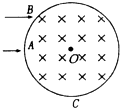 如图所示,在一个半径为R的圆形区域内存在垂直纸面向里的匀强磁场,O为圆心,一个电子以一定速度v沿AO方向(水平)射入磁场,经过时间t从O点正下方的C点射出磁场,另一电子以相同速度从磁场边界上的B点水平射入磁场,两速度方向与圆周在同一平面内,且A、B两点间圆弧长度为$\frac{π}{4}$R,则第二个电子在磁场中运动的时间为多少?
如图所示,在一个半径为R的圆形区域内存在垂直纸面向里的匀强磁场,O为圆心,一个电子以一定速度v沿AO方向(水平)射入磁场,经过时间t从O点正下方的C点射出磁场,另一电子以相同速度从磁场边界上的B点水平射入磁场,两速度方向与圆周在同一平面内,且A、B两点间圆弧长度为$\frac{π}{4}$R,则第二个电子在磁场中运动的时间为多少?
分析 第一个电子运动的轨道半径和磁场圆半径相等,根据轨迹的圆心角,可求出时间t.第二个电子的轨道半径与第一个电子相同,画出其运动轨迹,得到轨迹对应的圆心角,再解出时间.
解答  解:由题意知,第一个电子运动的轨道半径和磁场圆半径相等,在磁场中的偏向角为$\frac{π}{2}$,则 t=$\frac{T}{4}$
解:由题意知,第一个电子运动的轨道半径和磁场圆半径相等,在磁场中的偏向角为$\frac{π}{2}$,则 t=$\frac{T}{4}$
则电子圆周运动的周期为 T=4t
根据半径公式r=$\frac{mv}{qB}$知,两个电子的速度相等,则圆周运动的轨迹半径相等,由题意可知,第二个电子在磁场中运动的轨道半径也为R,如图所示,设第二个电子在磁场中运动轨迹所对应的圆心角为θ,则由几何关系可知,第二个电子在磁场中运动轨迹所对应的圆心角为 θ=$\frac{\frac{3π}{4}R}{R}$=$\frac{3}{4}π$
故第二个电子在磁场中运动的时间为 t′=$\frac{\frac{3}{4}π}{2π}$T=$\frac{3}{2}$t
答:第二个电子在磁场中运动的时间为$\frac{3}{2}$t.
点评 本题关键是描绘出电子的运动轨迹,确定出轨迹对应的圆心角,结合公式t=$\frac{θ}{2π}$T求解时间.

练习册系列答案
相关题目
1. 如图所示,有一对等量异种电荷分别位于空间中的a点和f点,以a点和f点为顶点作一正立方体,现在各顶点间移动一试探电荷,关于试探电荷受电场力和具有的电势能以下判断正确的是( )
如图所示,有一对等量异种电荷分别位于空间中的a点和f点,以a点和f点为顶点作一正立方体,现在各顶点间移动一试探电荷,关于试探电荷受电场力和具有的电势能以下判断正确的是( )
 如图所示,有一对等量异种电荷分别位于空间中的a点和f点,以a点和f点为顶点作一正立方体,现在各顶点间移动一试探电荷,关于试探电荷受电场力和具有的电势能以下判断正确的是( )
如图所示,有一对等量异种电荷分别位于空间中的a点和f点,以a点和f点为顶点作一正立方体,现在各顶点间移动一试探电荷,关于试探电荷受电场力和具有的电势能以下判断正确的是( )| A. | 在b点和d点受力大小相等,方向相同 | |
| B. | 在c点和h点受力大小相等,方向相同 | |
| C. | 在b点和d点电势能相等 | |
| D. | 在c点和h点电势能相等 |
10.设地球的半径为R0,质量为m的人造卫星在距离地面R0高处绕地球做匀速圆周运动,地球表面处的重力加速度为g,则下列说法中正确的是( )
| A. | 卫星的线速度为$\frac{\sqrt{2g{R}_{0}}}{2}$ | B. | 卫星的角速度是$\sqrt{\frac{g}{2{R}_{0}}}$ | ||
| C. | 卫星的向心加速度为$\frac{{g}_{0}}{2}$ | D. | 卫星的周期为4π$\sqrt{\frac{2{R}_{0}}{g}}$ |
14.地球可视为球体,其自转周期为T,在它的两极处,用弹簧秤测得一物体重为P,在赤道上,用弹簧秤测得同一物体重为0.9P,已知万有引力常量为G,则地球的平均密度是( )
| A. | $\frac{3π}{{T}^{2}G}$ | B. | $\frac{2.7π}{{T}^{2}G}$ | C. | $\frac{30π}{{T}^{2}G}$ | D. | $\frac{π}{{T}^{2}G}$ |
11.某同学通过以下步骤测出了一定高度落下的排球对地面的冲击力:将一张白纸铺在水平地面上,把棒球在水里浸湿,然后让排球从规定的高度自由落下,并在白纸上留下球的水印.再将印有水印的白纸铺在台秤上,将球放在纸上的水印中心,缓慢地压球,使排球与纸接触部分逐渐发生形变直至刚好遮住水印,记下此时台秤的示数即为冲击力的最大值.下列物理学习或研究中用到的方法与该同学的方法相同的是( )
| A. | 建立“合力与分力”的概念 | B. | 建立“点电荷”的概念 | ||
| C. | 建立“电场强度”的概念 | D. | 建立“电场线”的概念 |
8. 一矩形金属线圈在匀强磁场中垂直磁场的转轴匀速转动,产生的感应电动热与时间的关系如图所示,如果此圈和一个R=100Ω的电阻构成闭合电路,不计电路的其它电阻,下列叙述正确的是( )
一矩形金属线圈在匀强磁场中垂直磁场的转轴匀速转动,产生的感应电动热与时间的关系如图所示,如果此圈和一个R=100Ω的电阻构成闭合电路,不计电路的其它电阻,下列叙述正确的是( )
 一矩形金属线圈在匀强磁场中垂直磁场的转轴匀速转动,产生的感应电动热与时间的关系如图所示,如果此圈和一个R=100Ω的电阻构成闭合电路,不计电路的其它电阻,下列叙述正确的是( )
一矩形金属线圈在匀强磁场中垂直磁场的转轴匀速转动,产生的感应电动热与时间的关系如图所示,如果此圈和一个R=100Ω的电阻构成闭合电路,不计电路的其它电阻,下列叙述正确的是( )| A. | 交变电流的周期为0.02s | B. | 交变电流的电流有效值为1A | ||
| C. | 交变电流的电流最大值为1A | D. | 电阻R两端的最大电压为141V |
 如图所示,质量为M=9kg的足够长的木板放在光滑的水平面上,质量为m=1kg的可看成质点的滑块处在木板的最左端,开始木板与滑块以共同速度v0=1m/s向右匀速运动,设滑块与木板间的动摩擦因数为μ=0.1,g取10m/s2
如图所示,质量为M=9kg的足够长的木板放在光滑的水平面上,质量为m=1kg的可看成质点的滑块处在木板的最左端,开始木板与滑块以共同速度v0=1m/s向右匀速运动,设滑块与木板间的动摩擦因数为μ=0.1,g取10m/s2 如图所示,一个边长为a,电阻为R的等边三角形线框,在外力作用下,以速度v匀速穿过宽均为a的两个匀强磁场.这两个磁场的磁感应强度大小分别为2B和B,方向相反,线框运动方向与底边平行且与磁场边缘垂直.取逆时针方向的电流为正.若从图示位置开始计时,线框中产生的感应电流i与运动时间t之间的函数图象,下面四个图中正确的是( )
如图所示,一个边长为a,电阻为R的等边三角形线框,在外力作用下,以速度v匀速穿过宽均为a的两个匀强磁场.这两个磁场的磁感应强度大小分别为2B和B,方向相反,线框运动方向与底边平行且与磁场边缘垂直.取逆时针方向的电流为正.若从图示位置开始计时,线框中产生的感应电流i与运动时间t之间的函数图象,下面四个图中正确的是( )



 如图所示,重为G=3N的电灯用水平细线BC系于右侧墙上,电线AB与竖直方向的夹角为30°,求:(取$\sqrt{3}$=1.73)
如图所示,重为G=3N的电灯用水平细线BC系于右侧墙上,电线AB与竖直方向的夹角为30°,求:(取$\sqrt{3}$=1.73)