题目内容
如图,与水平面成45°角的平面MN将空间分成I和II两个区域.一质量为m、电荷量为q(q>0)的粒子以速度v从平面MN上的P点水平向右射入I区.粒子在I区运动时,只受到大小不变、方向竖直向下的电场作用,电场强度大小为E;在II区运动时,只受到匀强磁场的作用,磁感应强度大小为B,方向垂直于纸面向里.(粒子的重力可以忽略)求:(1)粒子首次下从I区进入II区时的速度大小和方向.
(2)粒子首次从II区离开时到出发点P的距离.

【答案】分析:(1)粒子在电场中做类平抛运动,由运动的合成与分解知识可求得粒子首次从I区进入II区时的速度大小和方向;
(2)粒子在电场中做匀速圆周运动,由洛仑兹力充当向心力可求得离开点到出发点之间的距离.
解答:解:(1)在电场中类平抛,到达MN时的位移沿MN方向,
tan45°=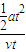
t=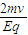
vy=at=2v
由平抛运动的位移关系可算出PP1间距离为: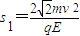 ,
,
到P1时的瞬时速度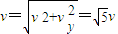 ,
,
v与竖直方向夹角α满足tanα= ,设v与MN的夹角为β,由α+β=45°,可得tanβ=
,设v与MN的夹角为β,由α+β=45°,可得tanβ= ;
;
(2)由牛顿第二定律可知:
Bqv=m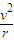
粒子在磁场中的轨道半径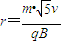 ,
,
而P1 P2间距离: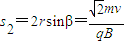
l=s1+s2
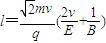
答:(1)粒子首次下从I区进入II区时的速度大小为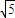 v;速度方向与MN夹角的正切值为
v;速度方向与MN夹角的正切值为 ;
;
(2)粒子首次从II区离开时到出发点P的距离为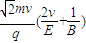 .
.
点评:对于类平抛运动可以直接利用速度夹角与位移夹角的正切值的关系直接求出速度与水平方向夹角.
(2)粒子在电场中做匀速圆周运动,由洛仑兹力充当向心力可求得离开点到出发点之间的距离.
解答:解:(1)在电场中类平抛,到达MN时的位移沿MN方向,
tan45°=
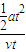
t=
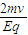
vy=at=2v
由平抛运动的位移关系可算出PP1间距离为:
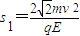 ,
,到P1时的瞬时速度
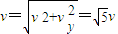 ,
,v与竖直方向夹角α满足tanα=
 ,设v与MN的夹角为β,由α+β=45°,可得tanβ=
,设v与MN的夹角为β,由α+β=45°,可得tanβ= ;
;(2)由牛顿第二定律可知:
Bqv=m
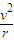
粒子在磁场中的轨道半径
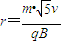 ,
,而P1 P2间距离:
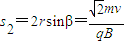
l=s1+s2
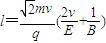
答:(1)粒子首次下从I区进入II区时的速度大小为
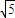 v;速度方向与MN夹角的正切值为
v;速度方向与MN夹角的正切值为 ;
;(2)粒子首次从II区离开时到出发点P的距离为
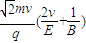 .
.点评:对于类平抛运动可以直接利用速度夹角与位移夹角的正切值的关系直接求出速度与水平方向夹角.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图,与水平面成45°角的平面MN将空间分成Ⅰ和Ⅱ两个区域.一质量为m、电荷量为q(q>0)的粒子以速度v0从平面MN上的P0点水平右射入I区.粒子在Ⅰ区运动时,只受到大小不变、方向竖直向下的电场作用,电场强度大小为E;在Ⅱ区运动时,只受到匀强磁场的作用,磁感应强度大小为B,方向垂直于纸面向里.求粒子首次从Ⅱ区离开时到出发点P0的距离.粒子的重力可以忽略.
如图,与水平面成45°角的平面MN将空间分成Ⅰ和Ⅱ两个区域.一质量为m、电荷量为q(q>0)的粒子以速度v0从平面MN上的P0点水平右射入I区.粒子在Ⅰ区运动时,只受到大小不变、方向竖直向下的电场作用,电场强度大小为E;在Ⅱ区运动时,只受到匀强磁场的作用,磁感应强度大小为B,方向垂直于纸面向里.求粒子首次从Ⅱ区离开时到出发点P0的距离.粒子的重力可以忽略.

 从平面MN上的
从平面MN上的 点水平右射入I区。粒子在I区运动时,只受到大小不变、方向竖直向下的电场作用,电场强度大小为E;在II区运动时,只受到匀强磁场的作用,磁感应强度大小为B,方向垂直于纸面向里。
点水平右射入I区。粒子在I区运动时,只受到大小不变、方向竖直向下的电场作用,电场强度大小为E;在II区运动时,只受到匀强磁场的作用,磁感应强度大小为B,方向垂直于纸面向里。