题目内容
1．
两个质量相等的带电小球A、B，在等长的绝缘细线作用下处于静止状态，其中小球A紧靠着光滑的绝缘墙壁，系小球A的细线呈竖直状态，系小球B的细线偏离竖直方向成θ角．若减小小球B的带电量，系统重新平衡后，下列说法正确的是（ ）| A． | θ增大 | |
| B． | 由于小球A的带电量不变，其受到的库仑力大小不变 | |
| C． | 小球A受到细线的拉力不变 | |
| D． | 小球B受到细线的拉力不变 |
分析 由库仑定律可确定其受库仑力变小，由B受力情况可确定θ角，及绳的拉力的变化．
解答 
解：A、由F=$K\frac{Qq}{{r}^{2}}$，可知F变小，小球平衡被打破，两者距离要变小，则θ变小，则A错误
B、D、小球B受力如图所示，两绝缘线的长度都是L，则△OAB是等腰三角形，由力的三角形与几何三角形相似，则$\frac{G}{T}=\frac{L}{L}$
即细线的拉力T与重力G相等，G=T，则D正确，而F=2Gsin$\frac{θ}{2}$，因θ变小，则F要变小．则B错误
C、对于A球：T+2Gsin$\frac{θ}{2}$$•sin\frac{θ}{2}$=G，因θ变小，则T变大，则C错误
故选：D
点评 对小球正确受力分析，应用平衡条件及库仑定律即可正确解题，解题时要注意△OAB是等腰三角形，注意数学知识的应用
练习册系列答案
相关题目
11．行星在太阳的引力作用下绕太阳公转，若把地球和水星绕太阳的运动轨迹都近似看作圆．已知地球绕太阳公转的半径大于水星绕太阳公转的半径，则下列判断正确的是（ ）
| A． | 地球的线速度大于水星的线速度 | |
| B． | 地球的角速度大于水星的角速度 | |
| C． | 地球的公转周期大于水星的公转周期 | |
| D． | 地球的向心加速度大于水星的向心加速度 |
12．图中为一物体在竖直方向上某段时间内运动图象（图象中取向上为正方向），以下说法正确的是（ ）
| A． | 0～2 s内物体处于失重状态 | |
| B． | 0～7 s内物体的平均速度为2.4 m/s | |
| C． | 0～7 s内物体的平均速度为2.0 m/s | |
| D． | 0～4 s内物体的机械能没有发生变化 |
如图所示，两光滑金属导轨，间距d=2m，在桌面上的部分是水平的，仅在桌面上有磁感应强度B=1T、方向竖直向下的有界磁场，电阻R=3Ω，桌面高H=0.8m，金属杆ab质量m=0.2kg，其电阻r=1Ω，从导轨上距桌面h=0.2m的高度处由静止释放，落地点距桌面左边缘的水平距离s=0.4m，取g=10m/s2，求：
如图，竖直平面内放着两根间距L=1m、电阻不计的足够长平行金属板M、N，两板间接一阻值R=2Ω的电阻，N板上有一小孔Q，在金属板M、N及CD上方有垂直纸面向里的磁感应强度B0=1T的有界匀强磁场，N板右侧区域KL上、下部分分别充满方向垂直纸面向外和向里的匀强磁场，磁感应强度大小分别为B1=3T和B2=2T．有一质量M=0.2kg、电阻r=1Ω的金属棒搭在MN之间并与MN良好接触，用输出功率恒定的电动机拉着金属棒竖直向上运动，当金属棒达最大速度时，在与Q等高并靠近M板的P点静止释放一个比荷$\frac{q}{m}$=1×104C/kg的正离子，经电场加速后，以v=200m/s的速度从Q点垂直于N板边界射入右侧区域．不计离子重力，忽略电流产生的磁场，取g=10m/s2．求：
6．
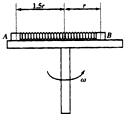如图所示，水平转台上的小物体A、B通过轻弹簧连接，并随转台一起匀速转动，A、B的质量分别为m、2m，A、B与转台的动摩擦因数都为μ，A、B离转台中心的距离分别为1.5r、r，已知弹簧的原长为1.5r，劲度系数为k，设最大静摩擦力等于滑动摩擦力，当B受到的摩擦力为零时，转台转动的角速度为（ ）
如图所示，水平转台上的小物体A、B通过轻弹簧连接，并随转台一起匀速转动，A、B的质量分别为m、2m，A、B与转台的动摩擦因数都为μ，A、B离转台中心的距离分别为1.5r、r，已知弹簧的原长为1.5r，劲度系数为k，设最大静摩擦力等于滑动摩擦力，当B受到的摩擦力为零时，转台转动的角速度为（ ）| A． | $\sqrt{\frac{k}{m}}$ | B． | $\sqrt{\frac{k}{2m}}$ | C． | $\sqrt{\frac{k}{2m}+\frac{μg}{2r}}$ | D． | $\sqrt{\frac{2k}{3m}+\frac{2μg}{3r}}$ |
13．
如图所示，n=100匝的一矩形线圈，面积S=0.01m2，内阻不计，绕垂直于磁感线的对称轴OO′以角速度ω=10πrad/s匀速转动，磁感应强度大小B=1T，则（取π2=10，二极管为理想二极管）（ ）
如图所示，n=100匝的一矩形线圈，面积S=0.01m2，内阻不计，绕垂直于磁感线的对称轴OO′以角速度ω=10πrad/s匀速转动，磁感应强度大小B=1T，则（取π2=10，二极管为理想二极管）（ ）| A． | 若负载为R=100Ω的电阻，负载的发热功率为2.5W | |
| B． | 若负载为R=100Ω的电阻，负载的发热功率为5W | |
| C． | 若负载为C=0.1μF的电容器，其耐压值不能小于10πV | |
| D． | 若负载为C=0.1μF的电容器，其耐压值不能小于5$\sqrt{2}$πV |
16．已知月球和同步卫星的公转周期之比为k，月球和地球同步卫星绕地球运动的轨道都视为圆，则下列说法正确的是（ ）
| A． | 月球和地球同步卫星的角速度之比为k-1 | |
| B． | 月球和地球同步卫星的向心加速度之比为k${\;}^{-\frac{1}{2}}$ | |
| C． | 月球和地球同步卫星的线速度之比为k${\;}^{\frac{1}{2}}$ | |
| D． | 月球和地球同步卫星的轨道半径之比为k${\;}^{\frac{1}{2}}$ |
17．关于平抛运动，下列说法不正确的是（ ）
| A． | 平抛运动是变加速曲线运动 | |
| B． | 平抛运动是匀变速曲线运动 | |
| C． | 平抛运动速度变化仅在竖直方向上 | |
| D． | 平抛运动在任意相等时间内速度的变化相同 |