题目内容
17. 如图所示,由喷泉中喷出的水柱,把一个重为W的垃圾桶倒顶在空中.水以速率v0、恒定的质量增率(即单位时间喷出的质量)$\frac{△m}{△t}$从地下射向空中.求垃圾桶可停留的最大高度.设水柱喷到桶底后以相同的速率反弹.
如图所示,由喷泉中喷出的水柱,把一个重为W的垃圾桶倒顶在空中.水以速率v0、恒定的质量增率(即单位时间喷出的质量)$\frac{△m}{△t}$从地下射向空中.求垃圾桶可停留的最大高度.设水柱喷到桶底后以相同的速率反弹.
分析 设垃圾桶可停留的最大高度为h.由运动学公式表示出h与速度的关系.研究极短时间内水受到的冲量,根据冲力等于垃圾桶的重力,求出水的速度,从而求得高度.
解答 解:设垃圾桶可停留的最大高度为h,并设水柱到达h高处的速率为v,则v满足:
v2-v02=-2gh
得 v2=v02-2gh
由动量定理得:在极短时间△t内,水受到的冲量为
F△t=2($\frac{△m}{△t}$•△t)v
解得 F=2$\frac{△m}{△t}$•v=2$\frac{△m}{△t}$$\sqrt{{v}_{0}^{2}-2gh}$
据题有 F=Mg
联立解得 h=$\frac{{v}_{0}^{2}}{2g}$-$\frac{{M}^{2}g}{8}(\frac{△t}{△m})^{2}$
答:垃圾桶可停留的最大高度是$\frac{{v}_{0}^{2}}{2g}$-$\frac{{M}^{2}g}{8}(\frac{△t}{△m})^{2}$.
点评 本题要理清题意,建立物理模型:竖直上抛运动和碰撞的综合,运用运动学公式和动量定理结合研究.

练习册系列答案
相关题目
1.作用在同一物体上的两个共点力,大小均为20N,它们的合力大小不可能的是( )
| A. | 0 N | B. | 20 N | C. | 40 N | D. | 50N |
5.以下关于运动学概念描述正确的是( )
| A. | 加速度是描述速度随时间变化快慢的物理量 | |
| B. | 加速度增大速度一定增大 | |
| C. | 加速度方向与速度方向一定相同 | |
| D. | 速度变化量越大,加速度越大 |
12.下列电场线中正确的有( )
| A. |  | B. |  | ||
| C. |  | D. |  |
6.如图所示是质量为1kg的滑块在水平面上做直线运动的v-t图象.下列判断正确的是( )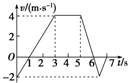

| A. | 在t=1s时,滑块的加速度为零 | |
| B. | 在4~6s时间内,滑块的平均速度为3 m/s | |
| C. | 在3~7s时间内,合力做功的平均功率为2 W | |
| D. | 在5~6s时间内,滑块受到的合力大小为2 N |


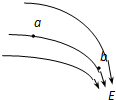 如图所示是电场中某区域的电场线,a、b两点的电场强度大小关系为Ea<Eb,同一试探电荷放在a、b两点所受到的电场力大小关系为Fa<Fb(选填“>”“<”或“=”)
如图所示是电场中某区域的电场线,a、b两点的电场强度大小关系为Ea<Eb,同一试探电荷放在a、b两点所受到的电场力大小关系为Fa<Fb(选填“>”“<”或“=”)