题目内容
1.第一宇宙速度又叫作环绕速度,第二宇宙速度又叫作逃逸速度.理论分析表明,天体的逃逸速度是环绕速度的$\sqrt{2}$倍.如果一个天体的质量足够大、半径足够小,则它的逃逸速度将非常大,即使连光都不能逃逸.我们把光都不能逃逸的天体称为黑洞.试分析对于一个质量为M的天体,若能够称之为黑洞,其半径R应该满足的条件.(已知万有引力常量G、光速c.)分析 根据题设条件,当天体的逃逸速度大于光速c时时,天体就成为黑洞.而逃逸速度是环绕速度的$\sqrt{2}$倍,根据万有引力提供向心力求出环绕速度,即可求出逃逸速度,就能得到R满足的条件.
解答 解:设第一宇宙速度为v1,有:
G$\frac{Mm}{{R}^{2}}$=m$\frac{{v}_{1}^{2}}{R}$
得:v1=$\sqrt{\frac{GM}{R}}$
由题得第二宇宙速度为:v2=$\sqrt{2}$v1
又由题:星体成为黑洞的条件为v2>c
即:$\sqrt{2}$•$\sqrt{\frac{GM}{R}}$>c
解得:R<$\frac{2GM}{{c}^{2}}$
答:对于一个质量为M的球状天体,当其半径R<$\frac{2GM}{{c}^{2}}$时会成为一个黑洞.
点评 本题是信息题或新概念题,首先要耐心、细心读题,抓住有效信息,其次建立物理模型.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
12. 2016年6月12号我国功发射了第23颗北斗导航卫星,该卫星为地球同步卫星.如图所示,发射地球同步卫星要经过三个阶段:先将卫星发射至近地圆轨道1,然后在Q点变轨至椭圆轨道2运行,最后再在P点变轨使卫星进入同步圆轨道3,对此发射过程,以下说法正确的是( )
2016年6月12号我国功发射了第23颗北斗导航卫星,该卫星为地球同步卫星.如图所示,发射地球同步卫星要经过三个阶段:先将卫星发射至近地圆轨道1,然后在Q点变轨至椭圆轨道2运行,最后再在P点变轨使卫星进入同步圆轨道3,对此发射过程,以下说法正确的是( )
 2016年6月12号我国功发射了第23颗北斗导航卫星,该卫星为地球同步卫星.如图所示,发射地球同步卫星要经过三个阶段:先将卫星发射至近地圆轨道1,然后在Q点变轨至椭圆轨道2运行,最后再在P点变轨使卫星进入同步圆轨道3,对此发射过程,以下说法正确的是( )
2016年6月12号我国功发射了第23颗北斗导航卫星,该卫星为地球同步卫星.如图所示,发射地球同步卫星要经过三个阶段:先将卫星发射至近地圆轨道1,然后在Q点变轨至椭圆轨道2运行,最后再在P点变轨使卫星进入同步圆轨道3,对此发射过程,以下说法正确的是( )| A. | 卫星在轨道1上运行的线速度小于在轨道3上运行的线速度 | |
| B. | 卫星在轨道2上经过P点时的加速度小于在轨道3上经过P点时的加速度 | |
| C. | 卫星由轨道1变轨进入轨道2,需要在Q点加速 | |
| D. | 卫星由轨道2变轨进入轨道3,需要在P点减速 |
6.质量相等的甲、乙两个物体,甲的速度是乙的速度的2倍,用EK1、EK2分别表示甲、乙两物体的动能,则( )
| A. | EK1=$\frac{1}{2}$EK2 | B. | EK1=2 EK2 | C. | EK1=$\frac{1}{4}$EK2 | D. | EK1=4 EK2 |
14.单摆作简谐运动的回复力是( )
| A. | .摆球的重力 | |
| B. | 摆球所受的重力沿圆弧切线方向的分力 | |
| C. | 摆球所受重力与悬线对摆球拉力的合力 | |
| D. | 悬线对摆球的拉力 |


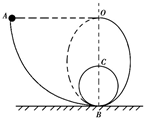 如图所示,光滑轨道ABCBO在同一竖直平面内,AB段为半径为R的四分之一圆弧,圆心在O点,该圆弧与圆轨道BCB及半椭圆形轨道BO相切于B点,现让一质量为m的小球以向下的初速度v0从A点进入轨道,结果在C点对圆轨道的压力为F,在O点对轨道的压力恰好为零.
如图所示,光滑轨道ABCBO在同一竖直平面内,AB段为半径为R的四分之一圆弧,圆心在O点,该圆弧与圆轨道BCB及半椭圆形轨道BO相切于B点,现让一质量为m的小球以向下的初速度v0从A点进入轨道,结果在C点对圆轨道的压力为F,在O点对轨道的压力恰好为零. 如图,竖直平面内固定一半径为R,口径很小的$\frac{3}{4}$圆形管道,管道的左半边内侧粗糙,其余部分光滑.与A管口紧挨放一个固定有轻弹簧的固定光滑斜面,弹簧自由伸长时上端与A管口齐平.一质量为m的小球(可视为质点)从A端正上方某处自由下落进入圆形管道,且经过管道最低点B处时小球对管壁的压力大小为其重力的9倍,小球继续运动,从管口C水平飞出后恰好沿斜面方向压缩弹簧,当弹簧被压缩最短时其形变量为x,求:
如图,竖直平面内固定一半径为R,口径很小的$\frac{3}{4}$圆形管道,管道的左半边内侧粗糙,其余部分光滑.与A管口紧挨放一个固定有轻弹簧的固定光滑斜面,弹簧自由伸长时上端与A管口齐平.一质量为m的小球(可视为质点)从A端正上方某处自由下落进入圆形管道,且经过管道最低点B处时小球对管壁的压力大小为其重力的9倍,小球继续运动,从管口C水平飞出后恰好沿斜面方向压缩弹簧,当弹簧被压缩最短时其形变量为x,求: