题目内容
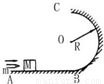
如图所示,ABC是光滑轨道,其中BC部分是半径为R的竖直放置的半圆轨道.一质量为M的小木块放在轨道水平部分,木块被水平飞来的质量为m的子弹射中,并滞留在木块中.若被击中的木块沿轨道能滑到最高点C,且对C点的压力大小为(M+m)g,求:(1)木块在C点时的速度.
(2)射入木块前,子弹的速度大小.
【答案】分析:(1)木块到达C点时,由重力和轨道的弹力的合力提供向心力,根据牛顿第二定律求解速度.
(2)子弹射入木块过程,系统的动量守恒.共同体从B到C的过程,只有重力做功,机械能守恒.根据动量守恒定律和机械能守恒定律列方程求解射入木块前子弹的速度大小.
解答: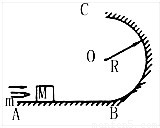 解:
解:
(1)木块到达C点时,由重力和轨道的弹力的合力提供向心力,根据牛顿第二定律得
(M+m)g+N=(M+m)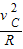
解得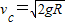
(2)子弹射入木块的过程,根据动量守恒定律得
mv=(M+m)v
共同体从B到C过程,由机械能守恒定律得
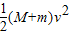 =(M+m)g?2R+
=(M+m)g?2R+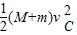
又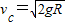
联立解得
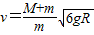
答:(1)木块在C点时的速度为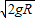 .
.
(2)射入木块前,子弹的速度大小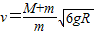 .
.
点评:对于圆周运动,常常是机械能守恒定律或动能定理与牛顿定律的综合.子弹射击木块过程,基本的规律是动量守恒.
(2)子弹射入木块过程,系统的动量守恒.共同体从B到C的过程,只有重力做功,机械能守恒.根据动量守恒定律和机械能守恒定律列方程求解射入木块前子弹的速度大小.
解答:
 解:
解:(1)木块到达C点时,由重力和轨道的弹力的合力提供向心力,根据牛顿第二定律得
(M+m)g+N=(M+m)
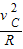
解得
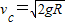
(2)子弹射入木块的过程,根据动量守恒定律得
mv=(M+m)v
共同体从B到C过程,由机械能守恒定律得
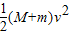 =(M+m)g?2R+
=(M+m)g?2R+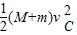
又
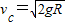
联立解得
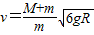
答:(1)木块在C点时的速度为
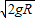 .
.(2)射入木块前,子弹的速度大小
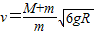 .
.点评:对于圆周运动,常常是机械能守恒定律或动能定理与牛顿定律的综合.子弹射击木块过程,基本的规律是动量守恒.

练习册系列答案
相关题目
 如图所示,ABC是一个透明的薄壁容器,内装液体,当光垂直射向AC面时,光在AB面恰好发生全反射,已知光在真空中的传播速度为c,求液体的折射率及光在该液体中传播速度多大?
如图所示,ABC是一个透明的薄壁容器,内装液体,当光垂直射向AC面时,光在AB面恰好发生全反射,已知光在真空中的传播速度为c,求液体的折射率及光在该液体中传播速度多大? (2006?南通一模)如图所示,ABC是由折射率为
(2006?南通一模)如图所示,ABC是由折射率为 如图所示,ABC是由折射率为
如图所示,ABC是由折射率为 如图所示,ABC是三棱镜的一个截面,其折射率为n=1.5.现有一细束平行于截面的光线沿MN方向射到棱镜的AB面上的N点,AN=NB=2cm,入射角的大小为i,且sini=0.75.已知真空中的光速c=3.0×108m/s,求:
如图所示,ABC是三棱镜的一个截面,其折射率为n=1.5.现有一细束平行于截面的光线沿MN方向射到棱镜的AB面上的N点,AN=NB=2cm,入射角的大小为i,且sini=0.75.已知真空中的光速c=3.0×108m/s,求: