题目内容
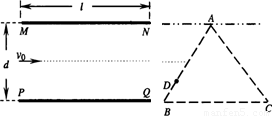
两块平行金属板MN、PQ水平放置,两板间距为d、板长为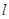 ,在平行板右侧的正三角形区域内存在着垂直纸面的匀强磁场,三角形底边BC与PQ在同一水平线上,顶点A与MN在同一水平线上,如图所示.一个质量为m、电量为+q的粒子沿两板中心线以初速度v0水平射入,若在两板间加某一恒定电压,粒子离开电场后垂直AB边从D点进入磁场,BD=
,在平行板右侧的正三角形区域内存在着垂直纸面的匀强磁场,三角形底边BC与PQ在同一水平线上,顶点A与MN在同一水平线上,如图所示.一个质量为m、电量为+q的粒子沿两板中心线以初速度v0水平射入,若在两板间加某一恒定电压,粒子离开电场后垂直AB边从D点进入磁场,BD=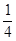 AB,并垂直AC边射出(不计粒子的重力).求:
AB,并垂直AC边射出(不计粒子的重力).求:
(1)两极板间电压;
(2)三角形区域内磁感应强度;
(3)若两板间不加电压,三角形区域内的磁场方向垂直纸面向外.要使粒子进入磁场区域后能从AB边射出,试求所加磁场的磁感应强度最小值.
(1)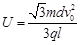 (2)
(2) (3)
(3)
【解析】
试题分析:(1)粒子在两块平行金属板间的电场中,沿水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动。粒子垂直AB边进入磁场,由几何知识得,粒子离开电场时速度偏转角θ=30°。 1分
根据类平抛运动的规律有:
l=v0t 1分
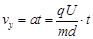 1分
1分
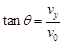 1分
1分
解得: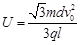 1分
1分
(2)由几何关系得: 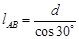 1分
1分
粒子在磁场中做圆周运动的轨道半径为: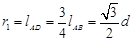 1分
1分
粒子进入磁场时的速率为: 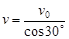 1分
1分
根据向心力公式有: 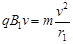 1分
1分
解得:
结合左手定则知,磁场方向垂直纸面向里。 1分
(3)若两板间不加电压,粒子将沿水平方向以速率v0从AB边的中点进入磁场。当粒子刚好与BC边相切时,磁感应强度最小。设磁感应强度的最小值为B2,由几何关系知,对应粒子的最大轨道半径r2为:
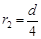 2分
2分
根据向心力公式有: 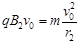 1分
1分
解得:  1分
1分
考点:考查了带电粒子在电磁场中的运动
点评:带电粒子在电场中的运动,综合了静电场和力学的知识,分析方法和力学的分析方法基本相同.先分析受力情况再分析运动状态和运动过程(平衡、加速、减速,直 线或曲线),然后选用恰当的规律解题.解决这类问题的基本方法有两种,第一种利用力和运动的观点,选用牛顿第二定律和运动学公式求解;第二种利用能量转化 的观点,选用动能定理和功能关系求解.
本题将有界磁场变为三角形磁场,仍然突出考查单一物体的多过程问题.带电粒子在电场、磁场中的运动,涉及到 电场、磁场的基本概念和规律,与力学中的牛顿运动定律和运动学公式、动能定理、平抛运动规律、匀速圆周运动规律等联系密切,综合性大,能充分考查考生的综 合分析能力和应用数学处理物理问题的能力.解此类问题的关键是做出带电粒子运动的轨迹图,抓住物理过程变化的转折点(列出对应的状态方程),找出粒子运动 的半径与磁场边界的约束关系.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
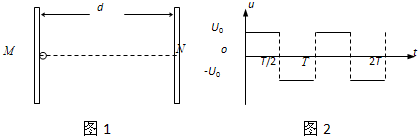
 如图所示,两块平行金属板MN间的距离为d,两板间电压u随时间t变化的规律如右图所示电压的绝对值为U0.t=0时刻M板的电势比N板低.在t=0时刻有一个电子从M板处无初速释放,经过1.5个周期刚好到达N板.电子的电荷量为e,质量为m.求:
如图所示,两块平行金属板MN间的距离为d,两板间电压u随时间t变化的规律如右图所示电压的绝对值为U0.t=0时刻M板的电势比N板低.在t=0时刻有一个电子从M板处无初速释放,经过1.5个周期刚好到达N板.电子的电荷量为e,质量为m.求: 如图所示,两块平行金属板MN、PQ竖直放置,两板间的电势差U=1.6×103 V,现将一质量m=3.0×10-2 kg、电荷量q=+4.0×10-5 C的带电小球从两板左上方的A点以初速度v0=4.0m/s水平抛出,已知A点距两板上端的高度h=0.45m,之后小球恰好从MN板上端内侧M点进入两板间匀强电场,然后沿直线运动到PQ板上的C点,不计空气阻力,取g=10m/s2,求:
如图所示,两块平行金属板MN、PQ竖直放置,两板间的电势差U=1.6×103 V,现将一质量m=3.0×10-2 kg、电荷量q=+4.0×10-5 C的带电小球从两板左上方的A点以初速度v0=4.0m/s水平抛出,已知A点距两板上端的高度h=0.45m,之后小球恰好从MN板上端内侧M点进入两板间匀强电场,然后沿直线运动到PQ板上的C点,不计空气阻力,取g=10m/s2,求: