��Ŀ����
1�� 2014��9��26�գ�ӡ�Ȼ���̽�����ɹ�����X�ǽ���������������Բ���˶��˶�����ΪT����֪���ǰ뾶Ϊr�����DZ����������ٶ�Ϊg��X����������ΪG����
2014��9��26�գ�ӡ�Ȼ���̽�����ɹ�����X�ǽ���������������Բ���˶��˶�����ΪT����֪���ǰ뾶Ϊr�����DZ����������ٶ�Ϊg��X����������ΪG������������
| A�� | ���ǵ������ɱ���Ϊ$\frac{{r}^{2}}{gG}$ | |
| B�� | ���ǵ������ɱ���Ϊ$\frac{4{r}^{2}}{G{T}^{2}}$ | |
| C�� | ���DZ����һ�����ٶȿɱ���Ϊ$\sqrt{gr}$ | |
| D�� | ����̽��������������½��Ӧ��������ı����й�� |
���� ���������ܵ�����������ϵ������������������г���ʽ������ǵ�������
���������Ƶ���������Բ���˶������������ṩ�������г���ʽ������ǵ�������
��� �⣺A�����������ܵ�����������ϵ�����������������$G\frac{Mm}{{r}^{2}}=mg$����M=$\frac{g{r}^{2}}{G}$����A����
C�����������Ƶ���������Բ���˶������������ṩ������$G\frac{Mm}{{r}^{2}}=m\frac{4{��}^{2}}{{T}^{2}}r$����$M=\frac{4{��}^{2}{r}^{3}}{G{T}^{2}}$����B����
C����һ�����ٶ�v=$\sqrt{\frac{GM}{r}}$=$\sqrt{gr}$����C��ȷ��
D������̽��������������½��Ӧ��ǰ�������٣��Ըı����й������D����
��ѡ��C��
���� ������Ҫ�������ǵ����֪ʶ���ܸ������������ṩԲ���˶���������������Բ���˶����������ǹ���뾶�Ĺ�ϵ��֪�������ܵ�����������ϵ�������������������

��ϰ��ϵ�д�
 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д�
�����Ŀ
12�������м���ͼ�У����������ķ����ж���ȷ���ǣ�������
| A�� |  | B�� |  | C�� |  | D�� |  |
9�� ��ͼ��ʾ������a��b��c�����糡�е����������棬���ڵ�����֮��ĵ��Ʋ���ȣ���Uab=Ubc��ʵ��Ϊһ��������ʵ���ڵ糡��������ͨ��������ʱ���˶��켣��P��Q�������켣�ϵ����㣬�ݴ˿�֪����˵���в���ȷ���ǣ�������
��ͼ��ʾ������a��b��c�����糡�е����������棬���ڵ�����֮��ĵ��Ʋ���ȣ���Uab=Ubc��ʵ��Ϊһ��������ʵ���ڵ糡��������ͨ��������ʱ���˶��켣��P��Q�������켣�ϵ����㣬�ݴ˿�֪����˵���в���ȷ���ǣ�������
 ��ͼ��ʾ������a��b��c�����糡�е����������棬���ڵ�����֮��ĵ��Ʋ���ȣ���Uab=Ubc��ʵ��Ϊһ��������ʵ���ڵ糡��������ͨ��������ʱ���˶��켣��P��Q�������켣�ϵ����㣬�ݴ˿�֪����˵���в���ȷ���ǣ�������
��ͼ��ʾ������a��b��c�����糡�е����������棬���ڵ�����֮��ĵ��Ʋ���ȣ���Uab=Ubc��ʵ��Ϊһ��������ʵ���ڵ糡��������ͨ��������ʱ���˶��켣��P��Q�������켣�ϵ����㣬�ݴ˿�֪����˵���в���ȷ���ǣ�������| A�� | �����������У�a�ĵ������ | |
| B�� | �����ʵ�ͨ��P��ʱ�ĵ����ܱ�Q��� | |
| C�� | �����ʵ�ͨ��P��ʱ�Ķ��ܱ�Q��� | |
| D�� | �����ʵ�ͨ��P��ʱ�ļ��ٶȱ�Q��� |
16��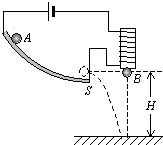 ���о�ƽ���˶�ʱ��Ϊ֤��ƽ���˶���ֱ����ķ��˶������������˶���ijͬѧ�������ͼ��ʾ��ʵ��װ�ã�С��A�ع�����£��뿪���ĩ��ʱײ�����ʽӴ�ʽ����S�����������ס��С��Bͬʱ�������䣬����λ��ͬһ�߶ȵ�A��B��������ͬʱ��أ�������˵����A�����뿪�������ֱ����ķ��˶������������˶��������г���һЩ����Ҫ������Ϊ��ȷ���ǣ�������
���о�ƽ���˶�ʱ��Ϊ֤��ƽ���˶���ֱ����ķ��˶������������˶���ijͬѧ�������ͼ��ʾ��ʵ��װ�ã�С��A�ع�����£��뿪���ĩ��ʱײ�����ʽӴ�ʽ����S�����������ס��С��Bͬʱ�������䣬����λ��ͬһ�߶ȵ�A��B��������ͬʱ��أ�������˵����A�����뿪�������ֱ����ķ��˶������������˶��������г���һЩ����Ҫ������Ϊ��ȷ���ǣ�������
 ���о�ƽ���˶�ʱ��Ϊ֤��ƽ���˶���ֱ����ķ��˶������������˶���ijͬѧ�������ͼ��ʾ��ʵ��װ�ã�С��A�ع�����£��뿪���ĩ��ʱײ�����ʽӴ�ʽ����S�����������ס��С��Bͬʱ�������䣬����λ��ͬһ�߶ȵ�A��B��������ͬʱ��أ�������˵����A�����뿪�������ֱ����ķ��˶������������˶��������г���һЩ����Ҫ������Ϊ��ȷ���ǣ�������
���о�ƽ���˶�ʱ��Ϊ֤��ƽ���˶���ֱ����ķ��˶������������˶���ijͬѧ�������ͼ��ʾ��ʵ��װ�ã�С��A�ع�����£��뿪���ĩ��ʱײ�����ʽӴ�ʽ����S�����������ס��С��Bͬʱ�������䣬����λ��ͬһ�߶ȵ�A��B��������ͬʱ��أ�������˵����A�����뿪�������ֱ����ķ��˶������������˶��������г���һЩ����Ҫ������Ϊ��ȷ���ǣ�������| A�� | ͨ�����ڹ��������ʹ���ĩ��ˮƽ | |
| B�� | ͨ����������װ�ã�ʹA���뿪���ĩ��ʱ��B���ͬһ�߶����� | |
| C�� | ÿ���ڹ���϶��ͷ�С��A��λ�ñ�����ͬһ�� | |
| D�� | ÿ���ڹ���϶��ͷ�С��A�������ɾ�ֹ�ͷ� | |
| E�� | ����ı�����װ�õĸ߶�H��ͬ����ʵ�� | |
| F�� | ���ø��ӹ⻬�Ĺ���������飬��������ȷ |
6�� ��ͼ������Ϊm�������Ϊֱ�������ε����ABC��AB�߿�����ֱǽ���ϣ���ABC=�ѣ������ǽ���Ķ�Ħ������Ϊ�̣�F�Ǵ�ֱ��б��BC�������������ǽ�������»�����Ħ�����Ĵ�СΪ��������
��ͼ������Ϊm�������Ϊֱ�������ε����ABC��AB�߿�����ֱǽ���ϣ���ABC=�ѣ������ǽ���Ķ�Ħ������Ϊ�̣�F�Ǵ�ֱ��б��BC�������������ǽ�������»�����Ħ�����Ĵ�СΪ��������
 ��ͼ������Ϊm�������Ϊֱ�������ε����ABC��AB�߿�����ֱǽ���ϣ���ABC=�ѣ������ǽ���Ķ�Ħ������Ϊ�̣�F�Ǵ�ֱ��б��BC�������������ǽ�������»�����Ħ�����Ĵ�СΪ��������
��ͼ������Ϊm�������Ϊֱ�������ε����ABC��AB�߿�����ֱǽ���ϣ���ABC=�ѣ������ǽ���Ķ�Ħ������Ϊ�̣�F�Ǵ�ֱ��б��BC�������������ǽ�������»�����Ħ�����Ĵ�СΪ��������| A�� | mg+Fcos�� | B�� | mg+Fsin�� | C�� | ��mg | D�� | ��Fcos�� |
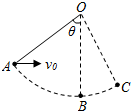 ��ͼ��һ��С�������O������ֱ������Բ���˶���B����Բ���˶�����͵㣬���ߵij�ΪL���ֽ�������A�㣬���߸պ���ֱ����������ֱ����ļн�Ϊ53�㣬��С��һ��ˮƽ���ҵij��ٶȣ����С��պ��ܵ���C�㣬С�������Ϊm�����������ٶ�Ϊg����sin53��=0.8��cos53��=0.6��
��ͼ��һ��С�������O������ֱ������Բ���˶���B����Բ���˶�����͵㣬���ߵij�ΪL���ֽ�������A�㣬���߸պ���ֱ����������ֱ����ļн�Ϊ53�㣬��С��һ��ˮƽ���ҵij��ٶȣ����С��պ��ܵ���C�㣬С�������Ϊm�����������ٶ�Ϊg����sin53��=0.8��cos53��=0.6�� �ڷ���ˮƽ����ǿ�糡�У�һ�����쳤�IJ�����ϸ�ߵ�һ������һ������Ϊm�Ĵ���С����һ�˹̶���O�㣮��С������ֱ��ϸ���볡ǿƽ�У�Ȼ�������ͷţ���֪С��ڵ���͵����һ�࣬������ֱ��������н�Ϊ�ȣ���ͼ������
�ڷ���ˮƽ����ǿ�糡�У�һ�����쳤�IJ�����ϸ�ߵ�һ������һ������Ϊm�Ĵ���С����һ�˹̶���O�㣮��С������ֱ��ϸ���볡ǿƽ�У�Ȼ�������ͷţ���֪С��ڵ���͵����һ�࣬������ֱ��������н�Ϊ�ȣ���ͼ������