题目内容
17. 图为初速度v0沿直线运动的物体的速度图象,其末速度为vt,在时间t0内,物体的平均速度$\overline v$,则$\overline v$>$\frac{{{v_0}+{v_t}}}{2}$(选填:“>”;“<”;“=”).
图为初速度v0沿直线运动的物体的速度图象,其末速度为vt,在时间t0内,物体的平均速度$\overline v$,则$\overline v$>$\frac{{{v_0}+{v_t}}}{2}$(选填:“>”;“<”;“=”).
分析 速度时间图线的切线斜率表示加速度,根据图线斜率的变化判断加速度的变化.连接图线的首末两点,该直线表示做匀加速直线运动,得出平均速度速度的大小,通过图线与时间轴围成的面积表示位移比较物体的平均速度与匀变速直线运动的平均速度大小.
解答 解:图线的斜率逐渐减小,知加速度随时间减小.连接图线首末两点,该直线表示物体做匀加速直线运动,平均速度:$\overline{v}$=$\frac{{v}_{0}+{v}_{t}}{2}$,因为变加速直线运动图线与时间轴围成的面积大于匀加速直线运动图线与时间轴围成的面积,即变加速直线运动的位移大于匀加速直线运动的位移,时间相等,则平均速度大于匀加速直线运动的平均速度,即$\overline{v}$>$\frac{{v}_{0}+{v}_{t}}{2}$.
故答案为:>
点评 解决本题的关键知道速度时间图线的切线斜率表示加速度,图线与时间轴围成的面积表示位移.注意要借助辅助线构造匀速直线运动后才能使用平均速度公式.$\overline{v}$=$\frac{{v}_{0}+{v}_{t}}{2}$,

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
7. 如图所示,长为L的轻杆,一端固定一个小球,另一端固定在光滑的水平轴上,使小球在竖直平面内作圆周运动,关于小球在最高点的速度v0下列说法中正确的是( )
如图所示,长为L的轻杆,一端固定一个小球,另一端固定在光滑的水平轴上,使小球在竖直平面内作圆周运动,关于小球在最高点的速度v0下列说法中正确的是( )
 如图所示,长为L的轻杆,一端固定一个小球,另一端固定在光滑的水平轴上,使小球在竖直平面内作圆周运动,关于小球在最高点的速度v0下列说法中正确的是( )
如图所示,长为L的轻杆,一端固定一个小球,另一端固定在光滑的水平轴上,使小球在竖直平面内作圆周运动,关于小球在最高点的速度v0下列说法中正确的是( )| A. | v0的最小值为零 | |
| B. | v0由零逐渐增大,向心力也逐渐增大 | |
| C. | 当v0由$\sqrt{gR}$值逐渐减小时,杆对小球的弹力仍然逐渐增大 | |
| D. | 当v0由$\sqrt{gR}$值逐渐增大时,杆对小球的弹力也逐渐增大 |
8. 如图所示,斜面上有a、b、c、d 四个点,ab=bc=cd,从a点以初动能E0水平抛出一个小球,它落在斜面上的b点,若小球从 a 点以初动能 2E0水平抛出,不计空气阻力,则下列判断正确的是( )
如图所示,斜面上有a、b、c、d 四个点,ab=bc=cd,从a点以初动能E0水平抛出一个小球,它落在斜面上的b点,若小球从 a 点以初动能 2E0水平抛出,不计空气阻力,则下列判断正确的是( )
 如图所示,斜面上有a、b、c、d 四个点,ab=bc=cd,从a点以初动能E0水平抛出一个小球,它落在斜面上的b点,若小球从 a 点以初动能 2E0水平抛出,不计空气阻力,则下列判断正确的是( )
如图所示,斜面上有a、b、c、d 四个点,ab=bc=cd,从a点以初动能E0水平抛出一个小球,它落在斜面上的b点,若小球从 a 点以初动能 2E0水平抛出,不计空气阻力,则下列判断正确的是( )| A. | 小球一定落在c点与d点之间 | |
| B. | 小球一定落在c点 | |
| C. | 小球落在斜面的运动方向与斜面的夹角一定相同 | |
| D. | 小球落在斜面的运动方向与斜面的夹角一定增大 |
5.某船要渡过300m宽的河,已知船相对水的速度始终为3m/s,河水的流速始终不变,大小为5m/s,下列说法中正确的是( )
| A. | 该船要渡河所用时间最少为100s | |
| B. | 该船渡河的最短位移是300m | |
| C. | 该船要用最短的时间渡河,它的轨迹为曲线 | |
| D. | 该船不可能沿垂直河岸的航线抵达对岸 |
12.如图是某一质点作直线运动的v-t图,由图可知,这个质点的运动情况是( )
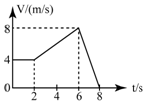

| A. | 前2秒是静止 | |
| B. | 2-6秒作的是匀加速运动,加速度是$\frac{4}{3}$m/s2 | |
| C. | 6-8秒作匀减速运动,加速度为-4m/s2 | |
| D. | 质点6秒末离出发点最远,8秒末回到出发点 |
2.用力F将木块紧按在竖直墙面上,木块所受的重力为8N,当水平力F为20N时,恰好匀速下滑,木块所受摩擦力的大小和木块与墙面间的动摩擦因数别为( )
| A. | 20N和0.4 | B. | 8N和0.4 | C. | 20N和1 | D. | 8N和1 |
6. 如图所示,物体从光滑斜面上的A点由静止开始下滑,经过B点后进入粗糙水平面(设经过B点前后速度大小不变),最后停在C点.每隔0.2秒通过速度传感器测量物体的瞬时速度大小,下表给出了部分测量数据.求:
如图所示,物体从光滑斜面上的A点由静止开始下滑,经过B点后进入粗糙水平面(设经过B点前后速度大小不变),最后停在C点.每隔0.2秒通过速度传感器测量物体的瞬时速度大小,下表给出了部分测量数据.求:
(1)物体在斜面加速度a1大小和水平面上的加速度a2大小;
(2)从A点达到C点的时间t;
(3)到达B点的瞬时速度vB大小;
(4)t=0.6s时瞬时速度大小v.
 如图所示,物体从光滑斜面上的A点由静止开始下滑,经过B点后进入粗糙水平面(设经过B点前后速度大小不变),最后停在C点.每隔0.2秒通过速度传感器测量物体的瞬时速度大小,下表给出了部分测量数据.求:
如图所示,物体从光滑斜面上的A点由静止开始下滑,经过B点后进入粗糙水平面(设经过B点前后速度大小不变),最后停在C点.每隔0.2秒通过速度传感器测量物体的瞬时速度大小,下表给出了部分测量数据.求:| t/(s) | 0.0 | 0.2 | 0.4 | … | 1.4 | 1.6 | … |
| v/(m/s) | 0.0 | 1.2 | 2.4 | … | 0.8 | 0.4 | … |
(2)从A点达到C点的时间t;
(3)到达B点的瞬时速度vB大小;
(4)t=0.6s时瞬时速度大小v.
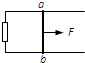 如图所示,位于水平面内的两根平行的光滑金属导轨处在匀强磁场中,磁场方向垂直于导轨所在的平面,导轨的一端与一电阻相连,金属杆ab放在导轨上并与导轨垂直,现用以平行于导轨的恒力F拉ab,使之由静止开始向右运动.金属杆ab和导轨的电阻不计,用E表示回路中的感应电动势,i表示回路中的感应电流,在i随时间增大的过程中,电阻消耗的瞬时功率( )
如图所示,位于水平面内的两根平行的光滑金属导轨处在匀强磁场中,磁场方向垂直于导轨所在的平面,导轨的一端与一电阻相连,金属杆ab放在导轨上并与导轨垂直,现用以平行于导轨的恒力F拉ab,使之由静止开始向右运动.金属杆ab和导轨的电阻不计,用E表示回路中的感应电动势,i表示回路中的感应电流,在i随时间增大的过程中,电阻消耗的瞬时功率( )