题目内容
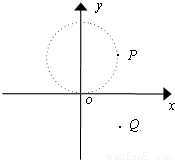
如图 (a)所示,x轴上方为垂直于平面xoy向里的匀强磁场,磁感应强度为B,x轴下方为方向平行于x轴但大小一定(设为E)、方向作周期性变化的匀强电场,在坐标点为(R、R)和第四象限中某点,各有质量为m、带电量为q的正点电荷P和Q,现使P在匀强磁场中开始做半径为R的匀速圆周运动,同时释放Q,要使两电荷总是以相同的速度同时通过y轴.求:(1)场强E的大小及其方向和变化周期T.
(2)在图 (b)中作出该电场变化的E-t图象(以释放电荷P时为初始时刻,x轴正方向作为场强的正方向),要求至少画出两个周期的图象.
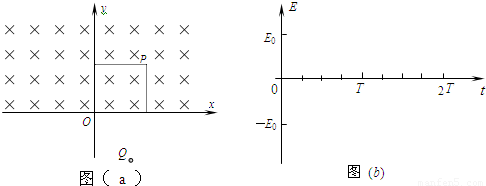
【答案】分析:P在磁场中做匀速圆周运动,洛伦兹力提供向心力,从而求出运动的速度和周期T;其次,粒子在T=n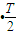 +
+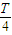 的时刻水平通过y轴,第一次通过y时的时间是
的时刻水平通过y轴,第一次通过y时的时间是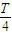 ,Q在前
,Q在前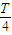 内做匀加速直线运动,根据运动学的方程和牛顿第二定律求出场强.
内做匀加速直线运动,根据运动学的方程和牛顿第二定律求出场强.
解答:解:(1)P在磁场中有:Bqv=m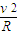 ,T1=
,T1=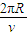
得:v=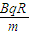 ,T1=
,T1=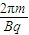
Q在电场中经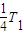 到达y轴,应有:v=
到达y轴,应有:v=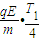
即: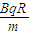 =
=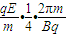 ,
,
∴E=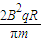
故电荷在通过y轴后先减速,经过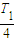 速度为0,然后返回做匀加速运动…所以电场变化的周期:电场变化周期T=T1=
速度为0,然后返回做匀加速运动…所以电场变化的周期:电场变化周期T=T1=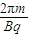
(2)作出该电场变化的E-t图象如图所示.
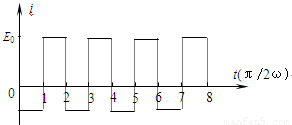
答:(1)场强E的大小为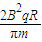 ,其方向变化的周期T为
,其方向变化的周期T为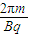 .
.
(2)作出该电场变化的E-t图象如图所示.
点评:解决该题的关键是判断出粒子通过y轴的时间与P运动周期的关系,抓住对称性和周期性是分析的技巧.
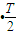 +
+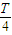 的时刻水平通过y轴,第一次通过y时的时间是
的时刻水平通过y轴,第一次通过y时的时间是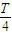 ,Q在前
,Q在前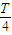 内做匀加速直线运动,根据运动学的方程和牛顿第二定律求出场强.
内做匀加速直线运动,根据运动学的方程和牛顿第二定律求出场强.解答:解:(1)P在磁场中有:Bqv=m
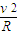 ,T1=
,T1=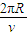

得:v=
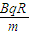 ,T1=
,T1=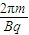
Q在电场中经
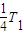 到达y轴,应有:v=
到达y轴,应有:v=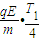
即:
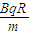 =
=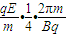 ,
,∴E=
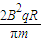
故电荷在通过y轴后先减速,经过
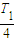 速度为0,然后返回做匀加速运动…所以电场变化的周期:电场变化周期T=T1=
速度为0,然后返回做匀加速运动…所以电场变化的周期:电场变化周期T=T1=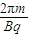
(2)作出该电场变化的E-t图象如图所示.

答:(1)场强E的大小为
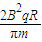 ,其方向变化的周期T为
,其方向变化的周期T为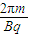 .
.(2)作出该电场变化的E-t图象如图所示.
点评:解决该题的关键是判断出粒子通过y轴的时间与P运动周期的关系,抓住对称性和周期性是分析的技巧.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
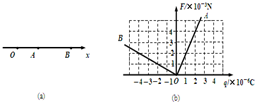 在如图(a)所示的x轴上有一个点电荷Q(图中未画出),A、B两点的坐标分别为0.2m和0.5m.放在A、B两点的检验电荷q1、q2受到的电场力跟检验电荷所带电量的关系如图(b)所示,规定x轴正方向为正.则B点的电场强度为
在如图(a)所示的x轴上有一个点电荷Q(图中未画出),A、B两点的坐标分别为0.2m和0.5m.放在A、B两点的检验电荷q1、q2受到的电场力跟检验电荷所带电量的关系如图(b)所示,规定x轴正方向为正.则B点的电场强度为 (2009?徐汇区二模)在如图(a)所示的x轴上有一个点电荷Q,轴上A、B两点的坐标分别为0.2m和0.5m.在A、B两点分别放置带正电的检验电荷(检验电荷间的相互作用可忽略不计),改变检验电荷的电量,检验电荷受到的电场力与所带电量的关系如图(b)所示,电场力的正方向与x轴正方向相同.则A点的电场强度大小为
(2009?徐汇区二模)在如图(a)所示的x轴上有一个点电荷Q,轴上A、B两点的坐标分别为0.2m和0.5m.在A、B两点分别放置带正电的检验电荷(检验电荷间的相互作用可忽略不计),改变检验电荷的电量,检验电荷受到的电场力与所带电量的关系如图(b)所示,电场力的正方向与x轴正方向相同.则A点的电场强度大小为 一简谐横波沿x轴正向传播,t=0时刻的波形如图(a)所示,x=0.60m处的质点的振动图线如图(b)所示,该质点在t=0时刻的运动方向沿y轴 (填“正向”或“负向”).已知该波的波长大于0.60m,则该波的波长为多少m( )
一简谐横波沿x轴正向传播,t=0时刻的波形如图(a)所示,x=0.60m处的质点的振动图线如图(b)所示,该质点在t=0时刻的运动方向沿y轴 (填“正向”或“负向”).已知该波的波长大于0.60m,则该波的波长为多少m( )
