题目内容
从一个足够长的光滑斜面的顶端先后由静止释放两个物体甲和乙,在匀加速下滑过程中( )
分析:甲乙两个物体都做匀加速直线运动,且加速度相同,根据匀加速直线运动位移时间关系及速度时间关系即可求解.
解答:解:设斜面与水平面的夹角为θ,根据对甲乙两个物体进行受力分析,根据牛顿第二定律得:
a=
=
=gsinθ
甲乙加速度相等.
设甲释放△t时间后,乙开始释放,则
△x=
at2-
a(t-△t)2=2at△t-
a△t2,可见随着时间的变化,位移差越来越大.
△v=at-a(t-△t)=a△t,可见速度差不随时间变化而变化.
故选C
a=
| F合 |
| m |
| mgsinθ |
| m |
甲乙加速度相等.
设甲释放△t时间后,乙开始释放,则
△x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
△v=at-a(t-△t)=a△t,可见速度差不随时间变化而变化.
故选C
点评:本题主要考查了匀加速直线运动位移时间关系及速度时间关系的直接应用,要知道甲乙加速度相同.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
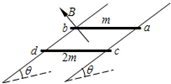 两根足够长的光滑金属导轨平行固定在倾角为θ的斜面上,它们的间距为d.磁感应强度为B的匀强磁场充满整个空间、方向垂直于斜面向上.两根金属杆ab、cd的质量分别为m和2m,垂直于导轨水平放置在导轨上,如图所示.设杆和导轨形成的回路总电阻为R而且保持不变,重力加速度为g.
两根足够长的光滑金属导轨平行固定在倾角为θ的斜面上,它们的间距为d.磁感应强度为B的匀强磁场充满整个空间、方向垂直于斜面向上.两根金属杆ab、cd的质量分别为m和2m,垂直于导轨水平放置在导轨上,如图所示.设杆和导轨形成的回路总电阻为R而且保持不变,重力加速度为g. 在倾角为30°的足够长的光滑斜面底端固定一个垂直于斜面的挡板,物体A,B用轻弹簧连接并放在斜面上,系统处于静止状态,如图所示,已知物体A的质量mA=2kg,物体B的质量mB=1kg,弹簧的劲度系数为k=100N/m,现在将物体B从静止状态沿斜面向下压10cm后释放,g取10m/s2,则在物体B运动的过程中( )
在倾角为30°的足够长的光滑斜面底端固定一个垂直于斜面的挡板,物体A,B用轻弹簧连接并放在斜面上,系统处于静止状态,如图所示,已知物体A的质量mA=2kg,物体B的质量mB=1kg,弹簧的劲度系数为k=100N/m,现在将物体B从静止状态沿斜面向下压10cm后释放,g取10m/s2,则在物体B运动的过程中( ) 如图,AB、CD是两根足够长的光滑固定平行金属导轨,两导轨间的距离为L,导轨平面与水平面的夹角为θ,在整个导轨平面内都有垂直于导轨平面斜向上方的匀强磁场,磁感应强度未知,在导轨的 AC端连接一个阻值为 R的电阻,一根质量为m、垂直于导轨放置的金属棒ab,(金属棒的阻值也为 R)从静止开始沿导轨下滑,已知金属棒下滑过程中的最大速度为vm(导轨电阻不计).
如图,AB、CD是两根足够长的光滑固定平行金属导轨,两导轨间的距离为L,导轨平面与水平面的夹角为θ,在整个导轨平面内都有垂直于导轨平面斜向上方的匀强磁场,磁感应强度未知,在导轨的 AC端连接一个阻值为 R的电阻,一根质量为m、垂直于导轨放置的金属棒ab,(金属棒的阻值也为 R)从静止开始沿导轨下滑,已知金属棒下滑过程中的最大速度为vm(导轨电阻不计).