题目内容
 (2011?安庆二模)如图所示,一竖直光滑绝缘的管内有一劲度系数为k的绝缘弹簧,其下端固定于地面,上端与一质量为m,带电量为+q的小球A相连,整个空间存在一竖直向上的匀强电场,小球A静止时弹簧恰为原长.另一质量也为m的不带电的绝缘小球B从距A为x0的P点由静止开始下落,与A发生碰撞后一起向下运动(全过程中小球A 的电量不发生变化,重力加速度为g).
(2011?安庆二模)如图所示,一竖直光滑绝缘的管内有一劲度系数为k的绝缘弹簧,其下端固定于地面,上端与一质量为m,带电量为+q的小球A相连,整个空间存在一竖直向上的匀强电场,小球A静止时弹簧恰为原长.另一质量也为m的不带电的绝缘小球B从距A为x0的P点由静止开始下落,与A发生碰撞后一起向下运动(全过程中小球A 的电量不发生变化,重力加速度为g).(1)若x0已知,试求B与A碰撞过程中损失的机械能;
(2)若x0未知,且B与A在最高点恰未分离,试求A、B运动到最高点时弹簧的形变量;
(3)在满足第(2)问的情况下,试求A、B运动过程中的最大速度.
分析:选择正确的研究对象.
分析物体的受力情况和运动过程.
由机械能守恒定律求得与A碰撞前B的速度.
根据动量守恒定律列出等式解决问题.
分析物体的受力情况和运动过程.
由机械能守恒定律求得与A碰撞前B的速度.
根据动量守恒定律列出等式解决问题.
解答:解:(1)设匀强电场的场强为E,在碰撞前A静止时有:
qE=mg ①
解得:E=
在与A碰撞前B的速度为v0,由机械能守恒定律得:
mgx0=
mv02
∴v0=
②
B与A碰撞后共同速度为v1,由动量守恒定律得:
mv0=2mv1 ③
∴v1=
v0
B与A碰撞过程中损失的机械能△E为:
△E═
mv02-
2mv12=
mgx0④
(2)A、B在最高点恰不分离,此时A、B加速度相等,且它们间的弹力为零,设此时弹簧的伸长量为x1,则:对B:
mg=ma ⑤
对A:mg+kx-qE=ma ⑥
所以弹簧的伸长量为:x1=
(3)A、B一起运动过程中合外力为零时,具有最大速度vm,设此时弹簧的压缩量为x2,则:
2mg-(qE+kx2)=0 ⑦
∴x2=
由于x1=x2,说明A、B在最高点处与合外力为零处弹簧的弹性势能相等,对此过程由能量守恒定律得:
(2mg-qE)(x1+x2)=
2mvm2 ⑧
解得:vm=g
答:(1)若x0已知,B与A碰撞过程中损失的机械能是
mgx0;
(2)若x0未知,且B与A在最高点恰未分离,A、B运动到最高点时弹簧的形变量是
;
(3)在满足第(2)问的情况下,A、B运动过程中的最大速度是g
.
qE=mg ①
解得:E=
| mg |
| q |
在与A碰撞前B的速度为v0,由机械能守恒定律得:
mgx0=
| 1 |
| 2 |
∴v0=
| 2gx0 |
B与A碰撞后共同速度为v1,由动量守恒定律得:
mv0=2mv1 ③
∴v1=
| 1 |
| 2 |
B与A碰撞过程中损失的机械能△E为:
△E═
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)A、B在最高点恰不分离,此时A、B加速度相等,且它们间的弹力为零,设此时弹簧的伸长量为x1,则:对B:
mg=ma ⑤
对A:mg+kx-qE=ma ⑥
所以弹簧的伸长量为:x1=
| mg |
| k |
(3)A、B一起运动过程中合外力为零时,具有最大速度vm,设此时弹簧的压缩量为x2,则:
2mg-(qE+kx2)=0 ⑦
∴x2=
| mg |
| k |
由于x1=x2,说明A、B在最高点处与合外力为零处弹簧的弹性势能相等,对此过程由能量守恒定律得:
(2mg-qE)(x1+x2)=
| 1 |
| 2 |
解得:vm=g
|
答:(1)若x0已知,B与A碰撞过程中损失的机械能是
| 1 |
| 2 |
(2)若x0未知,且B与A在最高点恰未分离,A、B运动到最高点时弹簧的形变量是
| mg |
| k |
(3)在满足第(2)问的情况下,A、B运动过程中的最大速度是g
|
点评:解决问题首先要清楚研究对象的运动过程.
我们要清楚运动过程中能量的转化,以便从能量守恒角度解决问题.
把动量守恒和能量守恒结合起来列出等式求解是常见的问题.
我们要清楚运动过程中能量的转化,以便从能量守恒角度解决问题.
把动量守恒和能量守恒结合起来列出等式求解是常见的问题.

练习册系列答案
相关题目
 (2011?安庆二模)如图所示,一个半径为R的圆轨道竖直固定在水平地面上,斜面AB与圆轨道在B
(2011?安庆二模)如图所示,一个半径为R的圆轨道竖直固定在水平地面上,斜面AB与圆轨道在B (2011?安庆二模)如图所示,在光滑的水平面上,一个质量为m的小球以速度v向东做匀速直线运动,小球运动的前方有一足够长的挡板,挡板与正东方向成300角.在某时刻加一水平恒力作用在小球上,小球经过路程L到达挡板时速度恰好为零,则所加恒力的大小是( )
(2011?安庆二模)如图所示,在光滑的水平面上,一个质量为m的小球以速度v向东做匀速直线运动,小球运动的前方有一足够长的挡板,挡板与正东方向成300角.在某时刻加一水平恒力作用在小球上,小球经过路程L到达挡板时速度恰好为零,则所加恒力的大小是( )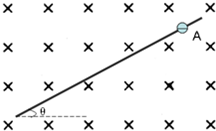 (2011?安庆二模)如图所示,空间存在垂直于纸面向里的磁感应强度为B的匀强磁场,场内有一绝缘的足够长的直杆,它与水平面的倾角为θ,一带电量为-q质量为m的带负电小球套在直杆上,从A点由静止沿杆下滑,小球与杆之间的动摩擦因数为μ,在小球以后的运动过程中,下列说法正确的是( )
(2011?安庆二模)如图所示,空间存在垂直于纸面向里的磁感应强度为B的匀强磁场,场内有一绝缘的足够长的直杆,它与水平面的倾角为θ,一带电量为-q质量为m的带负电小球套在直杆上,从A点由静止沿杆下滑,小球与杆之间的动摩擦因数为μ,在小球以后的运动过程中,下列说法正确的是( ) (2011?安庆二模)矩形导线框abcd放在磁场中,在外力控制下处于静止状态,如图(甲)所示.磁感线方向与导线框所在平面垂直,磁感应强度B随时间变化的图象如图(乙)所示.t=0时刻,磁感应强度的方向垂直导线框平面向里,在0~4s时间内,导线框ab边所受安培力随时间变化的图象(规定以向左为安培力正方向)可能是下列选项中的( )
(2011?安庆二模)矩形导线框abcd放在磁场中,在外力控制下处于静止状态,如图(甲)所示.磁感线方向与导线框所在平面垂直,磁感应强度B随时间变化的图象如图(乙)所示.t=0时刻,磁感应强度的方向垂直导线框平面向里,在0~4s时间内,导线框ab边所受安培力随时间变化的图象(规定以向左为安培力正方向)可能是下列选项中的( )