题目内容
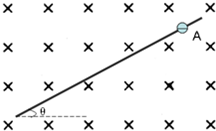（2011?安庆二模）如图所示，空间存在垂直于纸面向里的磁感应强度为B的匀强磁场，场内有一绝缘的足够长的直杆，它与水平面的倾角为θ，一带电量为-q质量为m的带负电小球套在直杆上，从A点由静止沿杆下滑，小球与杆之间的动摩擦因数为μ，在小球以后的运动过程中，下列说法正确的是（ ）分析：小球从A点由静止沿杆下滑，受到重力、支持力、洛伦兹力、摩擦力，根据牛顿第二定律表示出加速度，进而分析出最大速度和最大加速度及加速度的变化过程．
解答：解：小球开始下滑时有：mgsinθ-μ（mgcosθ-qvB）=ma，随v增大，a增大，
当v=
时，a达最大值gsinθ，
此时洛伦兹力等于mgcosθ，支持力等于0，此后随着速度增大，洛伦兹力增大，支持力增大，
此后下滑过程中有：mgsinθ-μ（qvB-mgcosθ）=ma，
随v增大，a减小，当vm=
时，
a=0．此时达到平衡状态，速度不变．
所以整个过程中，v先一直增大后不变；a先增大后减小，所以B对．
故选B．
当v=
| mgcosθ |
| qB |
此时洛伦兹力等于mgcosθ，支持力等于0，此后随着速度增大，洛伦兹力增大，支持力增大，
此后下滑过程中有：mgsinθ-μ（qvB-mgcosθ）=ma，
随v增大，a减小，当vm=
| mg(sinθ-μcosθ) |
| μqB |
a=0．此时达到平衡状态，速度不变．
所以整个过程中，v先一直增大后不变；a先增大后减小，所以B对．
故选B．
点评：解决本题的关键是正确地进行受力分析，根据受力情况，判断运动情况．
练习册系列答案
相关题目
（2011?安庆二模）如图所示，一个半径为R的圆轨道竖直固定在水平地面上，斜面AB与圆轨道在B
（2011?安庆二模）如图所示，在光滑的水平面上，一个质量为m的小球以速度v向东做匀速直线运动，小球运动的前方有一足够长的挡板，挡板与正东方向成300角．在某时刻加一水平恒力作用在小球上，小球经过路程L到达挡板时速度恰好为零，则所加恒力的大小是（ ）
（2011?安庆二模）矩形导线框abcd放在磁场中，在外力控制下处于静止状态，如图（甲）所示．磁感线方向与导线框所在平面垂直，磁感应强度B随时间变化的图象如图（乙）所示．t=0时刻，磁感应强度的方向垂直导线框平面向里，在0～4s时间内，导线框ab边所受安培力随时间变化的图象（规定以向左为安培力正方向）可能是下列选项中的（ ）