Question

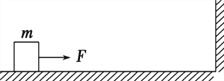
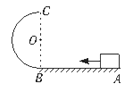
【题目】下面的装置可以探究外力做功和物体速度变化的关系．如图1所示，光滑斜槽轨道固定在水平桌面上，将斜槽从底端开始分成长度相等的五等份，使AB=BC=CD=DE=EF，让小球每次从不同等分点处释放，最后落在水平地面上．

（1）实验中，若小球从点释放运动至斜槽水平位置的过程中，外力做的功为，则小球从点释放运动至斜槽水平位置的过程中，外力做的功为___________．

（2）实验中，小球每次在斜槽上运动的长度记作，小球做平抛运动的水平位移记作，通过五组数据描点做出的图象2是一条过原点的直线．设小球运动到斜槽底端时的速度为，可以判断，外力做功与________（填）成正比．若斜槽的倾角为，小球抛出点距地面的高度为，则图象的斜率为___________（用表示）．

Answer 1

【答案】 （1） （2）

【解析】（1）根据几何关系可知，hFA=5hBA，对小球从F到A和B到A的两个过程，根据动能定理得：
W=mghFA，W′=mghBA，
解得：W′= W
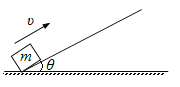
（2）小球从A点抛出后做平抛运动，下落的高度相等，则运动时间相等，则小球运动到斜槽底端时的速度 ①，
时间相等，所以v与x成正比，而根据图象可知，L与x2成正比，所以L与v2成正比，
小球抛出点距地面的高度为H，则运动时间 ②，
根据动能定理得：mgLsinθ=mv2③，
由①②③解得：
则L-x2图象的斜率 ．