题目内容
9.已知地球半径为R,地表重力加速度为g,同步卫星和“神州七号”卫星离地高度分别为h1和h2,求:(1)同步卫星和“神州七号”卫星的线速度之比.
(2)赤道上的物体和“神州七号”卫星的角速度之比.
(3)赤道上的物体和“神州七号”卫星的向心加速度之比.
分析 同步卫星定轨道(在赤道上方),定周期(与地球的自转周期相同),定速率、定高度.根据万有引力定律知向心力的大小;根据万有引力提供向心力,可知出同步卫星的轨道半径比沿赤道上空运动的近地卫星轨道半径大,进而判定v、ω、a的大小.
解答 解:(1)近地卫星、同步卫星的向心力是由万有引力提供,
$\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$
解得:v=$\sqrt{\frac{GM}{r}}$,
同步卫星和“神州七号”卫星离地高度分别为h1和h2,所以同步卫星和“神州七号”卫星的线速度之比是$\sqrt{\frac{R{+h}_{2}}{R{+h}_{1}}}$,
(2)根据万有引力提供向心力得:
$\frac{GMm}{{r}^{2}}$=mω2r
ω=$\sqrt{\frac{GM}{{r}^{3}}}$,
同步卫星、赤道上的物体的角速度相等,
所以赤道上的物体和“神州七号”卫星的角速度之比是$\sqrt{\frac{{(R{+h}_{2})}^{3}}{{(R{+h}_{1})}^{3}}}$,
(3)同步卫星、赤道上的物体的角速度相等,根据a=mω2r,
所以赤道上的物体和同步卫星的向心加速度之比是$\frac{R}{R{+h}_{1}}$,
根据万有引力提供向心力得:
$\frac{GMm}{{r}^{2}}$=ma
同步卫星和“神州七号”卫星的向心加速度之比是$\frac{{(R{+h}_{2})}^{2}}{{(R{+h}_{1})}^{2}}$,
所以赤道上的物体和“神州七号”卫星的向心加速度之比是$\frac{{R(R{+h}_{2})}^{2}}{{(R{+h}_{1})}^{3}}$,
答:(1)同步卫星和“神州七号”卫星的线速度之比是$\sqrt{\frac{R{+h}_{2}}{R{+h}_{1}}}$.
(2)赤道上的物体和“神州七号”卫星的角速度之比是$\sqrt{\frac{{(R{+h}_{2})}^{3}}{{(R{+h}_{1})}^{3}}}$.
(3)赤道上的物体和“神州七号”卫星的向心加速度之比是$\frac{{R(R{+h}_{2})}^{2}}{{(R{+h}_{1})}^{3}}$.
点评 解决本题的关键掌握同步卫星的特点:同步卫星定轨道(在赤道上方),定周期(与地球的自转周期相同),定速率、定高度.以及掌握万有引力提供向心力的公式.

 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案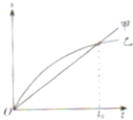 甲、乙两物体从同一起点出发,沿相同方向做直线运动,位移-时间图象如图所示,下列分析正确的是( )
甲、乙两物体从同一起点出发,沿相同方向做直线运动,位移-时间图象如图所示,下列分析正确的是( )| A. | 甲做匀变速运动 | B. | t0时刻甲、乙相遇 | ||
| C. | t0时刻甲、乙的速度相同 | D. | t0时刻甲、乙的加速度相同 |
| A. | 撤力后质点处于超重状态 | |
| B. | 2s末质点的速度大小为4m/s | |
| C. | 质点的加速度方向与初速度方向垂直 | |
| D. | 在任意一秒内质点的速度变化量均为1m/s,方向竖直向下 |
| A. | 赤道上物体与“三号卫星”的线速度之比为$\frac{{v}_{1}}{{v}_{3}}$=$\frac{R+h}{R}$ | |
| B. | 近地卫星与“三号卫星”的角速度之比为$\frac{{ω}_{2}}{{ω}_{3}}$=($\frac{R+h}{R}$)2 | |
| C. | 近地卫星与“三号卫星”的周期之比为$\frac{{T}_{2}}{{T}_{3}}$=$\sqrt{(\frac{R}{R+h})^{3}}$ | |
| D. | 赤道上物体与“三号卫星”的向心加速度之比为$\frac{{a}_{1}}{{a}_{3}}$=($\frac{R+h}{R}$)2 |
 我国未来将建立月球基地,并在绕月轨道上建造空间站.如图所示,关闭动力的航天飞机在月球引力作用下经椭圆轨道向月球靠近,并将与空间站在B处对接.已知空间站绕月轨道半径为r,周期为T,万有引力常量为G,下列说法中正确的是( )
我国未来将建立月球基地,并在绕月轨道上建造空间站.如图所示,关闭动力的航天飞机在月球引力作用下经椭圆轨道向月球靠近,并将与空间站在B处对接.已知空间站绕月轨道半径为r,周期为T,万有引力常量为G,下列说法中正确的是( )| A. | 图中航天飞机在飞向B处的过程中,加速度逐渐减小 | |
| B. | 航天飞机在B处由椭圆轨道进入空间站轨道必须点火减速 | |
| C. | 根据题中条件可以算出月球质量 | |
| D. | 根据题中条件可以算出空间站受到月球引力的大小 |

| A. | ωA<ωB | B. | ωA=ωB | C. | vA<vB | D. | vA=vB |
 小明放学经过一段平直的公路,看到一辆轿车出现故障熄火,马上帮着车主推车但没推动,如图所示.此轿车受到的力有( )
小明放学经过一段平直的公路,看到一辆轿车出现故障熄火,马上帮着车主推车但没推动,如图所示.此轿车受到的力有( )| A. | 重力、推力 | B. | 重力、支持力 | ||
| C. | 重力、推力、静摩擦力 | D. | 重力、支持力、推力和静摩擦力 |
 在闭合电路中,路端电压U与电流I的关系为U=E-Ir.以U为纵坐标,I为横坐标,作出U-I关系图象如图所示,A、B、C是图象上的三点,则外电路断开的状态对应图中的A点.若电源的电动势E=1.5V,内阻r=0.5Ω,则外电路断开时的路端电压为1.5V.
在闭合电路中,路端电压U与电流I的关系为U=E-Ir.以U为纵坐标,I为横坐标,作出U-I关系图象如图所示,A、B、C是图象上的三点,则外电路断开的状态对应图中的A点.若电源的电动势E=1.5V,内阻r=0.5Ω,则外电路断开时的路端电压为1.5V.