��Ŀ����
2�� ��ͼ��ʾΪһ�γ�ֱ���ά����ṹ�ɿ����������ʲ�ͬ����о�������ɣ���о��������n=$\sqrt{2}$������ȫ��������ʹ���ź�����о�д��䣬��������е��ٶ�c=3��108m/s��һ�����������������룬����˵����ȷ���ǣ�������
��ͼ��ʾΪһ�γ�ֱ���ά����ṹ�ɿ����������ʲ�ͬ����о�������ɣ���о��������n=$\sqrt{2}$������ȫ��������ʹ���ź�����о�д��䣬��������е��ٶ�c=3��108m/s��һ�����������������룬����˵����ȷ���ǣ�������| A�� | ��о��������С����� | |
| B�� | ���ڹ��ά��о�е��ٶ�Ϊ3��108m/s | |
| C�� | ������㣬������о�����棨��Ϊ����գ��䷢��ȫ������ٽ����45�� | |
| D�� | ���������������ά����Ƶ�ʱ�� |
���� ���ݹ��ȫ������������֪�������ʴ�С��ϵ��
��v=$\frac{c}{n}$����֪�����ڹ��ά��о�е��ٶȣ�
���ݹ�����䶨�ɣ����sinC=$\frac{1}{n}$����������ٽ�ǣ�
�ⷢ������ʱ��Ƶ�ʲ��䣬�ٶ��벨�������ȣ�
��� �⣺A������ӹ��ܽ��ʽ���������ʱ��������Ǵ����ٽ��ʱ���Żᷢ�����ȫ���䣬��A����
B������v=$\frac{c}{n}$=$\frac{3��1{0}^{8}}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}��1{0}^{8}$m/s����B����
C��������㣬����sinC=$\frac{1}{n}$�����C=45�㣬��C��ȷ��
D����������������ά����Ƶ�����DZ䣬��D����
��ѡ��C��
���� ���������䶨�ɣ����չ��ȫ���������������ٽ���������ʵĹ�ϵ��ע�ⷢ������ʱ��Ƶ�ʲ��䣬�ٶ��벨���ᷢ���仯��

��ϰ��ϵ�д�
�����Ŀ
12��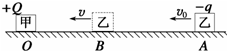 ��ͼ��ʾ��һ������Ϊ+Q�ĵ��ɼף��̶��ھ�Եˮƽ���ϵ�O�㣬��һ������Ϊ-q������Ϊm�ĵ����Ҵ�A���Գ��ٶ�v0�����ǵ��������������B��ʱ�ٶ���С��Ϊv����֪����������Ϊk����������ˮƽ��Ķ�Ħ������Ϊ�̣�AB�����ΪL��������˵����ȷ���ǣ�������
��ͼ��ʾ��һ������Ϊ+Q�ĵ��ɼף��̶��ھ�Եˮƽ���ϵ�O�㣬��һ������Ϊ-q������Ϊm�ĵ����Ҵ�A���Գ��ٶ�v0�����ǵ��������������B��ʱ�ٶ���С��Ϊv����֪����������Ϊk����������ˮƽ��Ķ�Ħ������Ϊ�̣�AB�����ΪL��������˵����ȷ���ǣ�������
 ��ͼ��ʾ��һ������Ϊ+Q�ĵ��ɼף��̶��ھ�Եˮƽ���ϵ�O�㣬��һ������Ϊ-q������Ϊm�ĵ����Ҵ�A���Գ��ٶ�v0�����ǵ��������������B��ʱ�ٶ���С��Ϊv����֪����������Ϊk����������ˮƽ��Ķ�Ħ������Ϊ�̣�AB�����ΪL��������˵����ȷ���ǣ�������
��ͼ��ʾ��һ������Ϊ+Q�ĵ��ɼף��̶��ھ�Եˮƽ���ϵ�O�㣬��һ������Ϊ-q������Ϊm�ĵ����Ҵ�A���Գ��ٶ�v0�����ǵ��������������B��ʱ�ٶ���С��Ϊv����֪����������Ϊk����������ˮƽ��Ķ�Ħ������Ϊ�̣�AB�����ΪL��������˵����ȷ���ǣ�������| A�� | OB��ľ���Ϊ $\sqrt{\frac{kQq}{��mg}}$ | |
| B�� | �ӿ�ʼ�˶���������֮ǰ��˲�䣬�ҵļ��ٶ���С | |
| C�� | ��A��B�Ĺ����У��糡���Ե��������Ĺ�ΪW=��mgL+$\frac{1}{2}$mv2-$\frac{1}{2}$mv02 | |
| D�� | ��A��B�Ĺ����У��ҵĵ����ܼ��� |
10����һ���������Ϊ����������32���������渽�����������ٶ��ǵ�����渽���������ٶȵ�2�������������ܶ�Լ�ǵ����ܶȵģ�������
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{4}$ | C�� | 2�� | D�� | 8�� |
11����֪��������ΪM���뾶ΪR����ת����ΪT������ͬ����������Ϊm����������ΪG���й�ͬ�����ǣ����б�����ȷ���ǣ�������
| A�� | �����ǵķ����ٶȴ���11.2km/s | |
| B�� | ���ǵ������ٶ�С�ڵ�һ�����ٶ� | |
| C�� | ��������ʱ�ܵ�����������СΪG$\frac{Mm}{{R}^{2}}$ | |
| D�� | �������е����ļ��ٶ�С�ڵ��������������ٶ� |
12�� �й�̽�¹���Ԥ����2015�����Ʒ���С�Ͳ������زգ��ɼ��ؼ���Ʒ�ص�����ͼΪ��������淵��ʱ���˶��켣ʾ��ͼ�������Ϊ������渽���Ļ��¹���������Ϊ����ת����Բ�������֪�����ƽ���ܶ�Ϊ�ѣ��뾶ΪR����������ΪG������˵����ȷ���ǣ�������
�й�̽�¹���Ԥ����2015�����Ʒ���С�Ͳ������زգ��ɼ��ؼ���Ʒ�ص�����ͼΪ��������淵��ʱ���˶��켣ʾ��ͼ�������Ϊ������渽���Ļ��¹���������Ϊ����ת����Բ�������֪�����ƽ���ܶ�Ϊ�ѣ��뾶ΪR����������ΪG������˵����ȷ���ǣ�������
 �й�̽�¹���Ԥ����2015�����Ʒ���С�Ͳ������زգ��ɼ��ؼ���Ʒ�ص�����ͼΪ��������淵��ʱ���˶��켣ʾ��ͼ�������Ϊ������渽���Ļ��¹���������Ϊ����ת����Բ�������֪�����ƽ���ܶ�Ϊ�ѣ��뾶ΪR����������ΪG������˵����ȷ���ǣ�������
�й�̽�¹���Ԥ����2015�����Ʒ���С�Ͳ������زգ��ɼ��ؼ���Ʒ�ص�����ͼΪ��������淵��ʱ���˶��켣ʾ��ͼ�������Ϊ������渽���Ļ��¹���������Ϊ����ת����Բ�������֪�����ƽ���ܶ�Ϊ�ѣ��뾶ΪR����������ΪG������˵����ȷ���ǣ�������| A�� | ���������������ٶ�Ϊg=$\frac{{4��G{R^2}��}}{3}$ | |
| B�� | ���ز��ƻ��¹�����˶�����ΪT=$\sqrt{\frac{3��}{G��}}$ | |
| C�� | ���ز��ڹ�����ϵ��������ڴ����ڹ�����ϵ��������� | |
| D�� | �������Ϸ��䷵�زս��뻷�¹���������С�����ٶ�Ϊv=$\frac{2R}{3}\sqrt{3�Ц�G}$ |
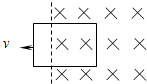 ��ͼ��ʾ���Ⱥ����ٶ�v1��v2��v1=2v2�������ٵذ�ͬһ��Ȧ��ͬһλ�������н���ǿ�ų��Ĺ����У����Ⱥ���������£�
��ͼ��ʾ���Ⱥ����ٶ�v1��v2��v1=2v2�������ٵذ�ͬһ��Ȧ��ͬһλ�������н���ǿ�ų��Ĺ����У����Ⱥ���������£� һ����Ϊm=2kg���������ڴֲڵ�ˮƽ�����ϣ��ܵ�һ����ʱ��仯��ˮƽ����F���ã�F��0-2s�ڵ�ͼ����ͼa��ʾ�������ٶ�v��ʱ��t�仯�Ĺ�ϵ��ͼb��ʾ����֪�����ˮƽ�����Ķ�Ħ��������=0.4��g=10m/s2��
һ����Ϊm=2kg���������ڴֲڵ�ˮƽ�����ϣ��ܵ�һ����ʱ��仯��ˮƽ����F���ã�F��0-2s�ڵ�ͼ����ͼa��ʾ�������ٶ�v��ʱ��t�仯�Ĺ�ϵ��ͼb��ʾ����֪�����ˮƽ�����Ķ�Ħ��������=0.4��g=10m/s2�� ��ͼ��Ϊij̽��С��Ϊ�ⶨ��Ħ�����������ã�ˮƽƽ̨���Ҷ˰�װ�����ʶ����֣�����ΪM=2.5kg�����A�����뻬�����L��ƽ̨�ϣ�����һ������������֣������������ӣ��Ҷ˹�����Ϊm=0.5kg��С��B������ֱʱ������סС��ʹ���ھ�����h����ֹ�����뻬�ּ��Ħ�����ƣ��������ٶ�Ϊg��gȡ10m/s2���������Ħ�������ڻ���Ħ�������ɾ�ֹ�ͷ�С��ϵͳ�˶�����С���С���ȼ�����������ĵ�ͬһ��Ƭ�϶���ع����Ƭ��ͼ���ң���ʾ������ʱÿ��1���ع�һ�Σ���С��ֱ��Ϊ20cm����ϵͳ���ٶȵ���0.4m/s2�����A��ƽ̨��Ķ�Ħ��������=0.152��
��ͼ��Ϊij̽��С��Ϊ�ⶨ��Ħ�����������ã�ˮƽƽ̨���Ҷ˰�װ�����ʶ����֣�����ΪM=2.5kg�����A�����뻬�����L��ƽ̨�ϣ�����һ������������֣������������ӣ��Ҷ˹�����Ϊm=0.5kg��С��B������ֱʱ������סС��ʹ���ھ�����h����ֹ�����뻬�ּ��Ħ�����ƣ��������ٶ�Ϊg��gȡ10m/s2���������Ħ�������ڻ���Ħ�������ɾ�ֹ�ͷ�С��ϵͳ�˶�����С���С���ȼ�����������ĵ�ͬһ��Ƭ�϶���ع����Ƭ��ͼ���ң���ʾ������ʱÿ��1���ع�һ�Σ���С��ֱ��Ϊ20cm����ϵͳ���ٶȵ���0.4m/s2�����A��ƽ̨��Ķ�Ħ��������=0.152��