题目内容
18. 如图所示,从A点以v0的初速度抛出一个小球,在离A点水平距离为s处有一堵高度为h的墙BC,要求小球能越过B点,问小球以怎样的角度抛出,才能使v0最小?
如图所示,从A点以v0的初速度抛出一个小球,在离A点水平距离为s处有一堵高度为h的墙BC,要求小球能越过B点,问小球以怎样的角度抛出,才能使v0最小?
分析 小球做斜抛运动,看成是沿v0方向的匀速直线运动和另一个自由落体运动的合运动,由矢量三角形法则和正弦定理两个方向分位移的关系,结合数学知识求解即可.
解答  解:将小球的斜抛运动,看成是沿v0方向的匀速直线运动和另一个自由落体运动的合运动,如图所示,在矢量三角形ABD中,由正弦定理,有:
解:将小球的斜抛运动,看成是沿v0方向的匀速直线运动和另一个自由落体运动的合运动,如图所示,在矢量三角形ABD中,由正弦定理,有:
$\frac{\frac{1}{2}g{t}^{2}}{sinα}$=$\frac{{v}_{0}t}{sinβ}$=$\frac{l}{sin(α+β)}$
由上式第一个等式可得 t=$\frac{2{v}_{0}sinα}{gsinβ}$
代入第二个等式,有 $\frac{2{v}_{0}^{2}sinα}{gsi{n}^{2}β}$=$\frac{l}{sin(α+β)}$
则得 2v02=$\frac{glsi{n}^{2}β}{sin(α+β)sinα}$=$\frac{glsi{n}^{2}β}{-cos(2α+β)+cosβ}$
当-cos(2α+β)有极大值1时,即2α+β=π时,v0有极小值
因2α+β=π,2α+φ+$\frac{π}{2}$=π
所以 α=$\frac{π}{4}$-$\frac{1}{2}$φ时,v0有最小值,且 φ=arctan$\frac{h}{s}$
答:小球以与AB连线成$\frac{π}{4}$-$\frac{1}{2}$φ(φ=arctan$\frac{h}{s}$)的角度抛出时,才能使v0最小.
点评 解决本题的关键能运用运动的合成法研究斜抛运动,根据三角形定则得到分位移的关系,运用数学知识求解极值.

练习册系列答案
相关题目
13. 如图所示,光源S从水面下向真空斜射出一束由红光和蓝光组成的复色光,在A点分成a、b两束,则下列说法正确的是( )
如图所示,光源S从水面下向真空斜射出一束由红光和蓝光组成的复色光,在A点分成a、b两束,则下列说法正确的是( )
 如图所示,光源S从水面下向真空斜射出一束由红光和蓝光组成的复色光,在A点分成a、b两束,则下列说法正确的是( )
如图所示,光源S从水面下向真空斜射出一束由红光和蓝光组成的复色光,在A点分成a、b两束,则下列说法正确的是( )| A. | b光是蓝光 | |
| B. | b光比a光更容易发生衍射现象 | |
| C. | 逐渐增大入射角,a光最先发生全反射 | |
| D. | 射出水面前a光的传播速度大,射出水面后二者传播速度一样大 |
3.自高为H的塔顶自由落下A物体的同时B物体自塔底以初速度v0竖直上抛,且A、B两物体在同一直线上运动.下面说法正确的是( )
| A. | 若v0>$\sqrt{gH}$,则两物体相遇时B物体正在上升途中 | |
| B. | 若v0=$\sqrt{gH}$,则两物体在地面相遇 | |
| C. | 若$\sqrt{\frac{gH}{2}}$<v0<$\sqrt{gH}$,则两物体相遇时B物体正在空中下落 | |
| D. | 若v0=$\sqrt{\frac{gH}{2}}$,则两物体不可能在空中相遇 |
10.一个阻值为2Ω的电阻,通过它的电流强度为2A,则下列说法正确的是( )
| A. | 1s内通过该电阻的电荷量为1C | B. | 该电阻1s内的发热量为4J | ||
| C. | 该电阻1s内的发热量为8J | D. | 该电阻发热功率是4W |
7.一辆汽车的额定功率为5×104W,若该汽车以额定功率启动,在平直高速公路上行驶时,受到的阻力位2×103N,则该汽车行驶的最大速度为( )
| A. | 25km/h | B. | 90km/h | C. | 50km/h | D. | 180km/h |
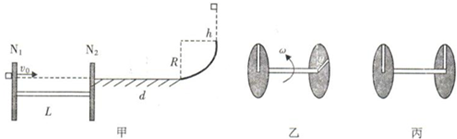
8. 如图甲所示的陀螺可在圆轨道的外侧旋转而不脱落,好像轨道对它施加了魔法一样,被称为“魔力陀螺”,该玩具深受孩子们的喜爱.其物理原理可等效为如图乙所示的模型:半径为R的磁性圆轨道竖直固定,质量为m的小铁球(视为质点)在轨道外侧转动,A、B两点分别为轨道上的最高、最低点.铁球受轨道的磁性引力始终指向圆心且大小不变,不计摩擦和空气阻力,重力加速度为g.下列说法正确的是( )
如图甲所示的陀螺可在圆轨道的外侧旋转而不脱落,好像轨道对它施加了魔法一样,被称为“魔力陀螺”,该玩具深受孩子们的喜爱.其物理原理可等效为如图乙所示的模型:半径为R的磁性圆轨道竖直固定,质量为m的小铁球(视为质点)在轨道外侧转动,A、B两点分别为轨道上的最高、最低点.铁球受轨道的磁性引力始终指向圆心且大小不变,不计摩擦和空气阻力,重力加速度为g.下列说法正确的是( )
 如图甲所示的陀螺可在圆轨道的外侧旋转而不脱落,好像轨道对它施加了魔法一样,被称为“魔力陀螺”,该玩具深受孩子们的喜爱.其物理原理可等效为如图乙所示的模型:半径为R的磁性圆轨道竖直固定,质量为m的小铁球(视为质点)在轨道外侧转动,A、B两点分别为轨道上的最高、最低点.铁球受轨道的磁性引力始终指向圆心且大小不变,不计摩擦和空气阻力,重力加速度为g.下列说法正确的是( )
如图甲所示的陀螺可在圆轨道的外侧旋转而不脱落,好像轨道对它施加了魔法一样,被称为“魔力陀螺”,该玩具深受孩子们的喜爱.其物理原理可等效为如图乙所示的模型:半径为R的磁性圆轨道竖直固定,质量为m的小铁球(视为质点)在轨道外侧转动,A、B两点分别为轨道上的最高、最低点.铁球受轨道的磁性引力始终指向圆心且大小不变,不计摩擦和空气阻力,重力加速度为g.下列说法正确的是( )| A. | 铁球可能做匀速圆周运动 | |
| B. | 铁球绕轨道转动时机械能守恒 | |
| C. | 铁球在A点的速度一定等于$\sqrt{gR}$ | |
| D. | 要使铁球不脱轨,轨道对铁球的磁性引力至少为5mg |
 某宇航员登上没有空气的行星后,将一小物体沿水平方向抛出,并采用频闪照相的方法记录下了小物体在运动过程中的4个位置A、B、C、D,如图所示,已知两次曝光的时间间隔为0.1s,照片中 每一小方格边长为5cm.则可知小物体抛出瞬间的速度为1m/s,该行星表面的重力加速度为5m/s2.
某宇航员登上没有空气的行星后,将一小物体沿水平方向抛出,并采用频闪照相的方法记录下了小物体在运动过程中的4个位置A、B、C、D,如图所示,已知两次曝光的时间间隔为0.1s,照片中 每一小方格边长为5cm.则可知小物体抛出瞬间的速度为1m/s,该行星表面的重力加速度为5m/s2. 用长为L的细线系一个质量为m的小球(小球可以视为质点),线的一端固定在空间的O点.先将小球拉至图中的P位置,使OP水平,然后无初速度释放小球,当小球绕O点转动150°到达Q位置时,细线碰到了一个固定的细钉子M,此后小球开始绕M做圆周运动,已知OM的长度是$\frac{4}{5}$L,求:
用长为L的细线系一个质量为m的小球(小球可以视为质点),线的一端固定在空间的O点.先将小球拉至图中的P位置,使OP水平,然后无初速度释放小球,当小球绕O点转动150°到达Q位置时,细线碰到了一个固定的细钉子M,此后小球开始绕M做圆周运动,已知OM的长度是$\frac{4}{5}$L,求: