��Ŀ����
��16�֣���ͼ��ʾ����xoyƽ���ڵڶ�����ij�������һ��������ǿ�ų������ų�����ֱxoyƽ������߽�ֱ�ƽ����x���y�ᡣһ�����Ϊe������Ϊm�ĵ��ӣ�������ԭ��ΪO���ٶ�v0����ڶ����ޣ��ٶȷ�����y���������45��ǣ������ų�ƫת��ͨ��P��0��a���㣬�ٶȷ���ֱ��y�ᣬ���Ƶ��ӵ�������

��1�����ų��ĴŸ�Ӧǿ�ȴ�СΪB0��������ڴų����˶���ʱ��t��
��2��Ϊʹ������������˶�����Ÿ�Ӧǿ�ȵĴ�СӦ�����������
��3�������ӵ���y����P��ʱ����ȥ������ǿ�ų���ͬʱ��y���Ҳ�ӷ���ֱxoyƽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB1����y�����ӷ���ֱxoyƽ���������ǿ�糡�������ڵڣ�k+1���δ������Ҿ���y�ᣨ����P��Ϊ��1�Σ�ʱǡ��ͨ������ԭ�㡣��y�����ų��Ÿ�Ӧǿ�ȴ�СB2���������̵��ӵ��˶�ʱ��t��
�⣺��1����ͼ����ʾ��
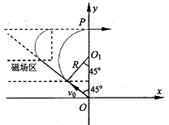
�����ڴų���ת���ĽǶ���=3��/4��
�˶�����T=2��m/eB0��t=��T/2�����������t=3��m/4eB0��
��2����Ÿ�Ӧǿ����СֵΪBmin����Ӧ���������뾶ΪR��Բ��O1.���У�ev0Bmin=m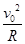 ��R+
��R+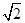 R=a
R=a
������ã�Bmin=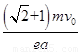 ��
��
�Ÿ�Ӧǿ�ȵĴ�СӦ���������Ϊ��B��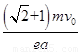 ��
��
��3���������y���Ҳ�������Բ���˶��İ뾶�ֱ�Ϊr1��r2�����У�
ev0B1=m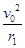 ��ev0B2=m
��ev0B2=m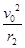 ��
��
��ͼ�ҵļ��ι�ϵ��֪��
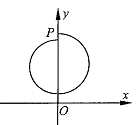
2k(r1-r2)=a
������ã�B2=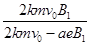 ��
��
�������y���Ҳ�������Բ���˶������ڷֱ�ΪT1��T2�����У�
T1=2��m/eB1��T2=2��m/eB2��
t=k(T1+T2)/2
������ã�t=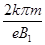 -
-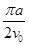 ��
��
���������������������ڴų����˶��Ĺ켣ͼ��Ӧ����������������������ͼ�м��ι�ϵ�������֪ʶ�з��̽��

 ��2013?����ģ�⣩��ͼ��ʾ����xoyƽ���ϣ�ֱ��OM��x��������н�Ϊ45�㣬ֱ��OM������ƽ��y�����ǿ�糡��������y�Ḻ����ֱ��OM�Ҳ���ڴ�ֱxoyƽ������ĴŸ�Ӧǿ��ΪB����ǿ�ų���һ������Ϊq����Ϊm����������ӣ�������������ԭ��O��x�����������ٶ�vo����ų����˺����Ӵ����ų���糡�ı߽����Σ�ǡ�ôӵ糡�лص�ԭ��O��������ͨ���߽�ʱ�����˶����ܱ߽��Ӱ�죩����
��2013?����ģ�⣩��ͼ��ʾ����xoyƽ���ϣ�ֱ��OM��x��������н�Ϊ45�㣬ֱ��OM������ƽ��y�����ǿ�糡��������y�Ḻ����ֱ��OM�Ҳ���ڴ�ֱxoyƽ������ĴŸ�Ӧǿ��ΪB����ǿ�ų���һ������Ϊq����Ϊm����������ӣ�������������ԭ��O��x�����������ٶ�vo����ų����˺����Ӵ����ų���糡�ı߽����Σ�ǡ�ôӵ糡�лص�ԭ��O��������ͨ���߽�ʱ�����˶����ܱ߽��Ӱ�죩����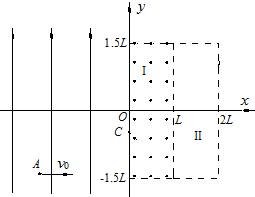 ��ͼ��ʾ����xOyƽ���y����������y�����������ǿ�糡��y���Ҳ�������ڴ��ڴŸ�Ӧǿ�ȴ�СB1=
��ͼ��ʾ����xOyƽ���y����������y�����������ǿ�糡��y���Ҳ�������ڴ��ڴŸ�Ӧǿ�ȴ�СB1= ��2006?���Ƹ۶�ģ����ͼ��ʾ����xoyƽ���ϣ�һ����ԭ��OΪ���ġ��뾶ΪR��Բ�������ڴ�����һ��ǿ�ų����ų��ĴŸ�Ӧǿ��ΪB������ֱ��xoyƽ�������O�㴦ԭ����ֹ��һ�����з����Ե�ԭ�Ӻ�--����
��2006?���Ƹ۶�ģ����ͼ��ʾ����xoyƽ���ϣ�һ����ԭ��OΪ���ġ��뾶ΪR��Բ�������ڴ�����һ��ǿ�ų����ų��ĴŸ�Ӧǿ��ΪB������ֱ��xoyƽ�������O�㴦ԭ����ֹ��һ�����з����Ե�ԭ�Ӻ�--���� ��ͼ��ʾ����xOyƽ���ϣ�һ����ԭ��OΪԲ�ģ��뾶Ϊ4R��ԭ�ʹų������ڴ�������ǿ�ų����ų��ķ���ֱ��ֽ����������꣨-2R��0����A����ֹ��һ�����з����Ե�ԭ�Ӻ˵�713N��ijʱ�̸ú˷���˥�䣬�ų�һ�������Ӻ�һ������ˣ���֪�����Ӵ�A�����ʱ�ٶȷ���ֱ��x�ᣬ�Һ���ͨ����y�ᣬ������˸պò��뿪�ų�����������Ӱ������Ӽ������ã�
��ͼ��ʾ����xOyƽ���ϣ�һ����ԭ��OΪԲ�ģ��뾶Ϊ4R��ԭ�ʹų������ڴ�������ǿ�ų����ų��ķ���ֱ��ֽ����������꣨-2R��0����A����ֹ��һ�����з����Ե�ԭ�Ӻ˵�713N��ijʱ�̸ú˷���˥�䣬�ų�һ�������Ӻ�һ������ˣ���֪�����Ӵ�A�����ʱ�ٶȷ���ֱ��x�ᣬ�Һ���ͨ����y�ᣬ������˸պò��뿪�ų�����������Ӱ������Ӽ������ã�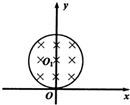 ��ͼ��ʾ����xOyƽ���ϣ���y���ϵ�OlΪԲ�ģ��뾶ΪR=0.3m��Բ�������ڣ��ֲ���һ������ֱ��xOyƽ������Ÿ�Ӧǿ�ȴ�СΪB=0.5T����ǿ�ų���һ���Ⱥ�
��ͼ��ʾ����xOyƽ���ϣ���y���ϵ�OlΪԲ�ģ��뾶ΪR=0.3m��Բ�������ڣ��ֲ���һ������ֱ��xOyƽ������Ÿ�Ӧǿ�ȴ�СΪB=0.5T����ǿ�ų���һ���Ⱥ�