题目内容
半径为a右端开小口的导体圆环和长为2a的导体直杆,单位长度电阻均为R0.圆环水平固定放置,整个内部区域分布着竖直向下的匀强磁场,磁感应强度为B.杆在圆环上以速度v平行于直径CD向右做匀速直线运动,杆始终有两点与圆环良好接触,从圆环中心O开始,杆的位置由θ确定,如图所示.则( )

| A.θ=0时,杆产生的电动势为2Bav | ||||
B.θ=
| ||||
C.θ=0时,杆受的安培力大小为
| ||||
D.θ=
|

解;A、θ=0时,杆产生的电动势E=BLv=2Bav,故A正确
B、θ=
时,根据几何关系得出此时导体棒的有效切割长度是a,所以杆产生的电动势为Bav,故B错误
C、θ=0时,由于单位长度电阻均为R0.所以电路中总电阻(2+π)aR0.
所以杆受的安培力大小F=BIL=B?2a
=
,故C错误
D、θ=
时,电路中总电阻是(
π+1)aR0
所以杆受的安培力大小F′=BI′L′=
,故D正确
故选AD.
B、θ=
| π |
| 3 |
C、θ=0时,由于单位长度电阻均为R0.所以电路中总电阻(2+π)aR0.
所以杆受的安培力大小F=BIL=B?2a
| 2Bav |
| (2+π)aR0 |
| 4B2av |
| (π+2)R0 |
D、θ=
| π |
| 3 |
| 5 |
| 3 |
所以杆受的安培力大小F′=BI′L′=
| 3B2av |
| (5π+3)R0 |
故选AD.

练习册系列答案
相关题目
 半径为a右端开小口的导体圆环和长为2a的导体直杆,单位长度电阻均为R0.圆环水平固定放置,整个内部区域分布着竖直向下的匀强磁场,磁感应强度为B.杆在圆环上以速度v平行于直径CD向右做匀速直线运动,杆始终有两点与圆环良好接触,从圆环中心O开始,杆的位置由θ确定,如图所示.则( )
半径为a右端开小口的导体圆环和长为2a的导体直杆,单位长度电阻均为R0.圆环水平固定放置,整个内部区域分布着竖直向下的匀强磁场,磁感应强度为B.杆在圆环上以速度v平行于直径CD向右做匀速直线运动,杆始终有两点与圆环良好接触,从圆环中心O开始,杆的位置由θ确定,如图所示.则( )| A、θ=0时,杆产生的电动势为Bav | ||||
B、θ=
| ||||
C、θ=0时,杆受的安培力大小为
| ||||
D、θ=
|
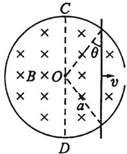 (2012?四川)半径为a右端开小口的导体圆环和长为2a的导体直杆,单位长度电阻均为R0.圆环水平固定放置,整个内部区域分布着竖直向下的匀强磁场,磁感应强度为B.杆在圆环上以速度v平行于直径CD向右做匀速直线运动,杆始终有两点与圆环良好接触,从圆环中心O开始,杆的位置由θ确定,如图所示.则( )
(2012?四川)半径为a右端开小口的导体圆环和长为2a的导体直杆,单位长度电阻均为R0.圆环水平固定放置,整个内部区域分布着竖直向下的匀强磁场,磁感应强度为B.杆在圆环上以速度v平行于直径CD向右做匀速直线运动,杆始终有两点与圆环良好接触,从圆环中心O开始,杆的位置由θ确定,如图所示.则( ) 半径为a右端开小口的导体圆环和长为2a的导体直杆,单位长度电阻均为R0.圆环水平固定放置,整个内部区域分布着竖直向下的匀强磁场,磁感应强度为B,杆在圆环上以速度v平行于直径CD向右做匀速直线运动,杆始终有两点与圆环良好接触,从圆环中心O开始,杆的位置由θ确定,如图所示.则θ=0时,杆产生的电动势为
半径为a右端开小口的导体圆环和长为2a的导体直杆,单位长度电阻均为R0.圆环水平固定放置,整个内部区域分布着竖直向下的匀强磁场,磁感应强度为B,杆在圆环上以速度v平行于直径CD向右做匀速直线运动,杆始终有两点与圆环良好接触,从圆环中心O开始,杆的位置由θ确定,如图所示.则θ=0时,杆产生的电动势为

 时,杆产生的电动势为
时,杆产生的电动势为




 时,杆产生的电动势为
时,杆产生的电动势为

