题目内容
12.兴趣小组的同学们利用如图1所示的装置“研究匀变速直线运动的规律”.他们将质量为m1的物体1与质量为m2的物体2(m1<m2)通过轻绳悬挂在定滑轮上,打点计时器固定在竖直方向上,物体1通过铁夹与纸带相连接.开始时物体1与物体2均处于静止状态,之后将它们同时释放.图2所示为实验中打点计时器打出的一条点迹清晰的纸带,O是打点计时器打下的第一个点,A、B、C、D…是按打点先后顺序依次选取的计数点,在相邻两个计数点之间还有四个点没有画出.打点计时器使用的交流电频率为50Hz.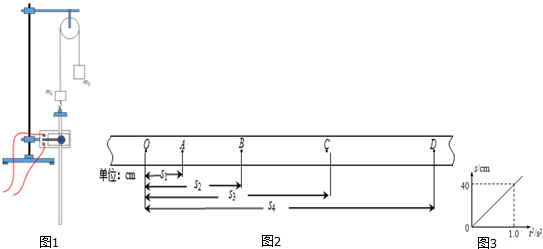
(1)相邻两计数点之间的时间间隔为0.1s;
(2)实验时要在接通打点计时器之后释放物体(选填“前”或“后”);
(3)将各计数点至O点的距离依次记为s1、s2、s3、s4…,测得s2=1.60cm,s4=6.40cm,请你计算打点计时器打下C点时物体的速度大小是0.24 m/s;
(4)同学们根据测出的物体1上升高度s与相应的时间t,描绘出如图3所示的s-t2图线,由此可以求出物体的加速度大小为0.8m/s2.
分析 根据相邻点时间间隔为0.02s,即可求解相邻两计数点之间的时间间隔;
先接通电源,后释放纸带;
中间时刻的瞬时速度等于这段时间内的平均速度;
根据图象的斜率,即可求解物体的加速度.
解答 解:(1)相邻两计数点之间的时间间隔为:T=0.02×5=0.1s;
(2)实验时要在接通打点计时器之后释放物体;
(3)C点的瞬时的速度为BD点的平均速度为:
vC=$\frac{{s}_{4}-{s}_{2}}{2T}$=$\frac{0.064-0.016}{2×0.1}$=0.24m/s
(4)根据运动学公式s=$\frac{1}{2}a{t}^{2}$,因此s-t2图线的斜率k=$\frac{a}{2}$,
那么a=2k=2×$\frac{0.4}{1}$=0.8m/s2;
故答案为:(1)0.1s; (2)后; (3)0.24; (4)0.8.
点评 考查计数点与实际打点的区别,注意先接通电源后,释放纸带,同时从纸带上求解速度和加速度是处理纸带的两个主要问题,一定要熟练掌握.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
19.下列有关地球的磁场表述正确的是( )
| A. | 地球的北极,磁极为N极 | B. | 地球的北极,磁极为S极 | ||
| C. | 地球的南极,磁极为S极 | D. | 地球不存在磁场 |
7.清洁工人在清洁城市道路时驾驶洒水车沿平直粗糙路面匀速行驶.当洒水车行驶到某一路口时开始洒水,若洒水车的速度保持不变,且所受阻力与车重成正比,则开始洒水后( )
| A. | 洒水车受到的牵引力保持不变 | B. | 洒水车受到的牵引力逐渐增大 | ||
| C. | 洒水车发动机的输出功率保持不变 | D. | 洒水车发动机的输出功率不断减小 |
17. 如图所示,在空间直角坐标系Oxyz中存在有沿x轴正方向的匀强磁场,在直角坐标系中选取如图所示的abc-a′b′c′棱柱形空间.通过面积S1(abb′a′所围的面积)、S2(acc′a′所围的面积)和S3(cbb′c′所围的面积)的磁通量分别为Φ1、Φ2和Φ3,则( )
如图所示,在空间直角坐标系Oxyz中存在有沿x轴正方向的匀强磁场,在直角坐标系中选取如图所示的abc-a′b′c′棱柱形空间.通过面积S1(abb′a′所围的面积)、S2(acc′a′所围的面积)和S3(cbb′c′所围的面积)的磁通量分别为Φ1、Φ2和Φ3,则( )
 如图所示,在空间直角坐标系Oxyz中存在有沿x轴正方向的匀强磁场,在直角坐标系中选取如图所示的abc-a′b′c′棱柱形空间.通过面积S1(abb′a′所围的面积)、S2(acc′a′所围的面积)和S3(cbb′c′所围的面积)的磁通量分别为Φ1、Φ2和Φ3,则( )
如图所示,在空间直角坐标系Oxyz中存在有沿x轴正方向的匀强磁场,在直角坐标系中选取如图所示的abc-a′b′c′棱柱形空间.通过面积S1(abb′a′所围的面积)、S2(acc′a′所围的面积)和S3(cbb′c′所围的面积)的磁通量分别为Φ1、Φ2和Φ3,则( )| A. | Φ1=Φ2 | B. | Φ1>Φ2 | C. | Φ1>Φ3 | D. | Φ3>Φ2 |
4.“神舟十号”飞船发射后,经过多次变轨进入距地面高度为h的圆形轨道.已知飞船质量为m,地球半径为R,地球表面的重力加速度为g.设飞船进入圆形轨道后运动时的动能为EK,则( )
| A. | Ek=$\frac{mg{R}^{2}}{2(R+h)}$ | B. | Ek=$\frac{1}{2}$mg(R+h) | C. | Ek=$\frac{1}{2}$mgR | D. | Ek=mgh |
1.下列物理量中,属于矢量的是( )
| A. | 位移 | B. | 质量 | C. | 时间 | D. | 速率 |
2.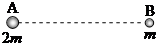 相距为d、质量分别为2m和m的两颗恒星A和B组成双星系统,在万有引力作用下各自绕它们连线上的某一固定点,在同一平面内做匀速圆周运动.设两颗恒星的转动半径分别为RA、RB,速度大小分别为vA、vB,动能分别为EkA、EkB,引力常量为G,则下列关系中正确的是( )
相距为d、质量分别为2m和m的两颗恒星A和B组成双星系统,在万有引力作用下各自绕它们连线上的某一固定点,在同一平面内做匀速圆周运动.设两颗恒星的转动半径分别为RA、RB,速度大小分别为vA、vB,动能分别为EkA、EkB,引力常量为G,则下列关系中正确的是( )
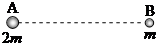 相距为d、质量分别为2m和m的两颗恒星A和B组成双星系统,在万有引力作用下各自绕它们连线上的某一固定点,在同一平面内做匀速圆周运动.设两颗恒星的转动半径分别为RA、RB,速度大小分别为vA、vB,动能分别为EkA、EkB,引力常量为G,则下列关系中正确的是( )
相距为d、质量分别为2m和m的两颗恒星A和B组成双星系统,在万有引力作用下各自绕它们连线上的某一固定点,在同一平面内做匀速圆周运动.设两颗恒星的转动半径分别为RA、RB,速度大小分别为vA、vB,动能分别为EkA、EkB,引力常量为G,则下列关系中正确的是( )| A. | RA=2RB | B. | vA=2vB | C. | EkA=EkB | D. | EkA+EkB=$\frac{G{m}^{2}}{d}$ |
 某同学到实验室用油膜法测油酸分子直径,实验主要步骤如下:
某同学到实验室用油膜法测油酸分子直径,实验主要步骤如下: