题目内容
如图，在竖直平面内的3/4圆弧形光滑轨道半径为10m，A端与圆心O等高，AD为水平面，B端在O的正上方．一个小球自A点正上方由静止释放，自由下落至A点进入圆轨道，到达B点时对轨道的压力恰好为零．g取10m/s2．求：（1）释放点距A点的竖直高度．
（2）落点C与A点的水平距离．
【答案】分析：（1）通过小球到达B点时对轨道的压力恰好为零，根据牛顿第二定律求出B点的速度，结合机械能守恒定律求出释放点距A点的竖直高度．
（2）根据B点的速度和高度，通过平抛运动的规律求出水平位移，从而求出落点C与A点的水平距离．
解答：解：（1）若小球在B点时速度为VB，由小球到达B点时对轨道的压力恰好为零，有
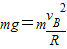①
若释放点距A点的竖直高度为h，由机械能守恒定律有：
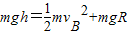②
由①②式并代入数据解得：h=15m．
（2）小球在B点以水平速度VB做平抛运动，
竖直方向有：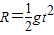
③
水平方向有：soc=vBt ④，
由③④式并代入数据解得：soc=14.1m
落点C与A点的水平距离sAC=soc-soA=14.1-10m=4.1m．
答：（1）释放点距A点的竖直高度为15m．
（2）落点C与A点的水平距离尾4.1m．
点评：本题考查了自由落体运动、圆周运动和平抛运动，综合考查了牛顿第二定律和机械能守恒定律，综合性较强，是一道好题．
（2）根据B点的速度和高度，通过平抛运动的规律求出水平位移，从而求出落点C与A点的水平距离．
解答：解：（1）若小球在B点时速度为VB，由小球到达B点时对轨道的压力恰好为零，有
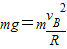①若释放点距A点的竖直高度为h，由机械能守恒定律有：
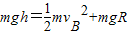②由①②式并代入数据解得：h=15m．
（2）小球在B点以水平速度VB做平抛运动，
竖直方向有：
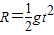③水平方向有：soc=vBt ④，
由③④式并代入数据解得：soc=14.1m
落点C与A点的水平距离sAC=soc-soA=14.1-10m=4.1m．
答：（1）释放点距A点的竖直高度为15m．
（2）落点C与A点的水平距离尾4.1m．
点评：本题考查了自由落体运动、圆周运动和平抛运动，综合考查了牛顿第二定律和机械能守恒定律，综合性较强，是一道好题．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
如图ABCD为竖直平面内的光滑轨道，BCD部分刚好为半个圆周，半径为R，其下端与水平部分AB相切，可看成质点的小物块质量为m，从A点自静止开始在水平力作用下运动到B点，到B点后撤去该水平力，物块继续沿轨道运动，通过轨道的最高点（D点）飞出，正好落在A点，不计一切摩擦和空气阻力，下列结论正确的是（ ）
如图，在竖直平面内的3/4圆弧形光滑轨道半径为10m，A端与圆心O等高，AD为水平面，B端在O的正上方．一个小球自A点正上方由静止释放，自由下落至A点进入圆轨道，到达B点时对轨道的压力恰好为零．g取10m/s2．求：
如图，在竖直平面内，光滑的圆弧轨道EA和BC与粗糙的水平轨道AB相切于A点和B点，相切处平滑．B是BC圆弧最低点，C与圆心O等高，BC圆弧半径R=1m．EA圆弧的半径r＞2m，E是圆弧EA最高点，h=2m．现有一个质量为m=0.1kg的小物块（可视为质点），从C点的正上方D点处自由下落，DC距离H=4m，物块与水平面AB之间的动摩擦因数μ=0.5．取g=10m/s2．求：
如图，在竖直平面内有一固定光滑轨道，其中AB部分是倾角为37°的直轨道，BCD部分是以O为圆心、半径为R的圆弧轨道，两轨道相切于B点，D点与O点等高，A点在D点的正下方．质量为m的小球在沿斜面向上的拉力F作用下，从A点由静止开始做变加速直线运动，到达B点时撤去外力．已知小球刚好能沿圆轨道经过最高点C，然后经过D点落回到A点．已知sin37°=0.6，cos37°=0.8，重力加速度大小为g．求