题目内容
3.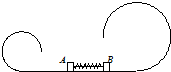 如图所示,一光滑轨道由水平轨道和圆弧形轨道构成,放在竖直平面内,圆弧形轨道半径分别为R和2R,在水平轨道上有A、B两物体,A、B中间隔有一轻弹簧,用细线连接A、B并使轻弹簧处于压缩状态.若剪断细线,A、B两物体能分别运动到左右两圆弧形轨道的最高点,且对轨道压力都为零.若不计任何摩擦,则A、B两物体的质量mA和mB之比为$\sqrt{2}$:1.
如图所示,一光滑轨道由水平轨道和圆弧形轨道构成,放在竖直平面内,圆弧形轨道半径分别为R和2R,在水平轨道上有A、B两物体,A、B中间隔有一轻弹簧,用细线连接A、B并使轻弹簧处于压缩状态.若剪断细线,A、B两物体能分别运动到左右两圆弧形轨道的最高点,且对轨道压力都为零.若不计任何摩擦,则A、B两物体的质量mA和mB之比为$\sqrt{2}$:1.
分析 能到达半圆形轨道最高点的临界条件是v≥$\sqrt{gr}$,恰好能通过最高点说明在最高点重力完全提供向心力,系统满足动量守恒,据此求解即可.
解答 解:相互作用的系统满足动量守恒,以A的速度方向为正方向,得:
mAvA-mBvB=0
最高点:对轨道的压力为0,所以根据牛顿第二定律:
A:mAg=$\frac{{{m}_{A}v}_{1}^{2}}{R}$
B:mBg=$\frac{{{m}_{B}v}_{2}^{2}}{2R}$
根据动能定理有:
$\frac{{{m}_{A}v}_{A}^{2}}{2}$-$\frac{{{m}_{A}v}_{1}^{2}}{2}$=2mAgR
$\frac{{{m}_{B}v}_{B}^{2}}{2}$-$\frac{{{m}_{B}v}_{2}^{2}}{2}$=4mBgR
联立解得mA:mB=$\sqrt{2}$:1
故答案为:$\sqrt{2}$:1,
点评 小球刚好到达圆管形轨道最高点的条件是:到达最高点时速度为零;应用牛顿第二定律、动量守恒定律即可正确解题.

练习册系列答案
相关题目
6. 在如图所示的电路中,电源电动势为E,内电阻为r,C为电容器,R0为定值电阻,R为滑动变阻器.开关闭合后,灯泡L能正常发光当滑动变阻器的滑片向左移动时下列判断正确的是( )
在如图所示的电路中,电源电动势为E,内电阻为r,C为电容器,R0为定值电阻,R为滑动变阻器.开关闭合后,灯泡L能正常发光当滑动变阻器的滑片向左移动时下列判断正确的是( )
 在如图所示的电路中,电源电动势为E,内电阻为r,C为电容器,R0为定值电阻,R为滑动变阻器.开关闭合后,灯泡L能正常发光当滑动变阻器的滑片向左移动时下列判断正确的是( )
在如图所示的电路中,电源电动势为E,内电阻为r,C为电容器,R0为定值电阻,R为滑动变阻器.开关闭合后,灯泡L能正常发光当滑动变阻器的滑片向左移动时下列判断正确的是( )| A. | R两端的电压变小 | B. | 灯泡L变暗 | ||
| C. | 电容器C的电荷量将减小 | D. | 有电流向右流过R0 |
14.一小球从静止开始做匀加速直线运动,在第5s内的位移比第3s内的位移多0.2m,则下列说法正确的是( )
| A. | 小球加速度为0.2m/s2 | B. | 小球第4s内的平均速度为0.45m/s | ||
| C. | 小球第4s的初速度为0.3m/s | D. | 前3s内的位移是0.6m |
8.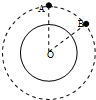 如图所示,一卫星在某一轨道上绕地心O做匀速圆周运动,轨道半径为r.经过时间t该卫星从位置A运行到位置B,∠AOB=60°.设地球半径为R,地球表面重力加速度为g.则下列说法中正确的是( )
如图所示,一卫星在某一轨道上绕地心O做匀速圆周运动,轨道半径为r.经过时间t该卫星从位置A运行到位置B,∠AOB=60°.设地球半径为R,地球表面重力加速度为g.则下列说法中正确的是( )
 如图所示,一卫星在某一轨道上绕地心O做匀速圆周运动,轨道半径为r.经过时间t该卫星从位置A运行到位置B,∠AOB=60°.设地球半径为R,地球表面重力加速度为g.则下列说法中正确的是( )
如图所示,一卫星在某一轨道上绕地心O做匀速圆周运动,轨道半径为r.经过时间t该卫星从位置A运行到位置B,∠AOB=60°.设地球半径为R,地球表面重力加速度为g.则下列说法中正确的是( )| A. | 卫星的加速度为$\frac{{R}^{2}g}{{r}^{2}}$ | |
| B. | 在卫星返回地面的过程中万有引力减弱重力增大 | |
| C. | 卫星由位置A运动到位置B需要的时间为$\frac{πr}{3R}$$\sqrt{\frac{r}{g}}$ | |
| D. | 卫星由位置A运动到位置B的过程中万有引力做功为零 |
15. 如图所示,将一束塑料包扎带一端打结,另一端撕成细条后,用手迅速捋细条,观察到细条散开了,则产生这种现象的原因是( )
如图所示,将一束塑料包扎带一端打结,另一端撕成细条后,用手迅速捋细条,观察到细条散开了,则产生这种现象的原因是( )
 如图所示,将一束塑料包扎带一端打结,另一端撕成细条后,用手迅速捋细条,观察到细条散开了,则产生这种现象的原因是( )
如图所示,将一束塑料包扎带一端打结,另一端撕成细条后,用手迅速捋细条,观察到细条散开了,则产生这种现象的原因是( )| A. | 细条之间相互感应起电,相互排斥散开 | |
| B. | 撕成细条后,所受重力减小,细条自然松散 | |
| C. | 撕成细条后,由于空气浮力作用,细条散开 | |
| D. | 由于摩擦起电,细条带同种电荷,相互排斥散开 |
 如图所示为一玻璃球的截面图,其半径为R,O为球体的球心,AB为截面圆的直径.在A点放一个能发某种单色光的点光源,照射球体内各个方向,只有部分光能从球体中射出,在此截面上,只有圆弧NBN′上有光射出,NN′连线垂直AB.已知从M点折射出的光线恰好平行AB,AM与AB的夹角为θ,求N、N′两点间的距离.
如图所示为一玻璃球的截面图,其半径为R,O为球体的球心,AB为截面圆的直径.在A点放一个能发某种单色光的点光源,照射球体内各个方向,只有部分光能从球体中射出,在此截面上,只有圆弧NBN′上有光射出,NN′连线垂直AB.已知从M点折射出的光线恰好平行AB,AM与AB的夹角为θ,求N、N′两点间的距离.