��Ŀ����
8��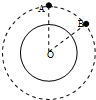 ��ͼ��ʾ��һ������ijһ������Ƶ���O������Բ���˶�������뾶Ϊr������ʱ��t�����Ǵ�λ��A���е�λ��B����AOB=60�㣮�����뾶ΪR����������������ٶ�Ϊg��������˵������ȷ���ǣ�������
��ͼ��ʾ��һ������ijһ������Ƶ���O������Բ���˶�������뾶Ϊr������ʱ��t�����Ǵ�λ��A���е�λ��B����AOB=60�㣮�����뾶ΪR����������������ٶ�Ϊg��������˵������ȷ���ǣ�������| A�� | ���ǵļ��ٶ�Ϊ$\frac{{R}^{2}g}{{r}^{2}}$ | |
| B�� | �����Ƿ��ص���Ĺ������������������������� | |
| C�� | ������λ��A�˶���λ��B��Ҫ��ʱ��Ϊ$\frac{��r}{3R}$$\sqrt{\frac{r}{g}}$ | |
| D�� | ������λ��A�˶���λ��B�Ĺ�����������������Ϊ�� |
���� �ڵ����������������������ȣ����������ṩ����Բ���˶���������������ͨ���������˶��������˶���ʵ�ֹ��λ�õĵ�����
��� �⣺A���ڵ����������������������ȣ������Ǵ����������ṩԲ���˶������������У�
$G\frac{Mm}{{R}_{\;}^{2}}=mg$��$G\frac{Mm}{{r}_{\;}^{2}}=ma$������ʽ�ɵ��������ǵļ��ٶȴ�С��Ϊ$a=\frac{g{R}_{\;}^{2}}{{r}_{\;}^{2}}$����A��ȷ��
B�������ڷ��ص���Ĺ����У�����ĵľ����С������������������$F=G\frac{Mm}{{r}_{\;}^{2}}$��֪������������Խ������������������ٶ�Խ������Խ��B����
C����A֪�����ǵ����ļ��ٶ�a=$\frac{{R}_{\;}^{2}}{{r}_{\;}^{2}}g$=$\frac{4{��}_{\;}^{2}}{{T}_{\;}^{2}}r$���ɵ����ǵ�����$T=2��\frac{r}{R}\sqrt{\frac{r}{g}}$�����Դ�A�˶���B����ʱ��t=$\frac{60��}{360��}T=\frac{��r}{3R}\sqrt{\frac{r}{g}}$����C��ȷ��
D������1������Բ���˶����������ṩԲ���˶���������������ʼ�����ٶȷ���ֱ�����������������Dz���������D��ȷ��
��ѡ��ACD��
���� ������Ҫ��������������Ӧ�����⣬���������������������������ȣ�������������������Բ���˶����������ṩ��������

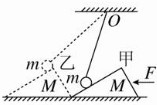 ��ͼ��ʾ��С��m��һ�������쳤������ϸ��˩ס������O�㣬С������һ��б�治�⻬��б��M�ϣ���ˮƽ��F�����ƶ�б��M�ڹ⻬ˮƽ��������λ�ü��������ƶ���λ���ң��ڴ˹����У���ȷ��˵���ǣ�������
��ͼ��ʾ��С��m��һ�������쳤������ϸ��˩ס������O�㣬С������һ��б�治�⻬��б��M�ϣ���ˮƽ��F�����ƶ�б��M�ڹ⻬ˮƽ��������λ�ü��������ƶ���λ���ң��ڴ˹����У���ȷ��˵���ǣ�������| A�� | M��m���Ħ������m������ | |
| B�� | M��m���Ħ������m������ | |
| C�� | F��M�����Ĺ���m��M�����Ĺ��ľ���ֵ��� | |
| D�� | M��m��ĵ�����m������ |
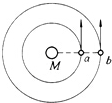 ��ͼ��a��b��ij����M���������ǣ����������幫ת������ΪTa��Tb��ijһʱ���������˶���ͼʾλ�ã��ҹ�ת������ͬ��
��ͼ��a��b��ij����M���������ǣ����������幫ת������ΪTa��Tb��ijһʱ���������˶���ͼʾλ�ã��ҹ�ת������ͬ��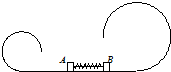 ��ͼ��ʾ��һ�⻬�����ˮƽ�����Բ���ι�����ɣ�������ֱƽ���ڣ�Բ���ι���뾶�ֱ�ΪR��2R����ˮƽ�������A��B�����壬A��B�м����һ�ᵯ�ɣ���ϸ������A��B��ʹ�ᵯ�ɴ���ѹ��״̬��������ϸ�ߣ�A��B�������ֱܷ��˶���������Բ���ι������ߵ㣬�ҶԹ��ѹ����Ϊ�㣮�������κ�Ħ������A��B�����������mA��mB֮��Ϊ$\sqrt{2}$��1��
��ͼ��ʾ��һ�⻬�����ˮƽ�����Բ���ι�����ɣ�������ֱƽ���ڣ�Բ���ι���뾶�ֱ�ΪR��2R����ˮƽ�������A��B�����壬A��B�м����һ�ᵯ�ɣ���ϸ������A��B��ʹ�ᵯ�ɴ���ѹ��״̬��������ϸ�ߣ�A��B�������ֱܷ��˶���������Բ���ι������ߵ㣬�ҶԹ��ѹ����Ϊ�㣮�������κ�Ħ������A��B�����������mA��mB֮��Ϊ$\sqrt{2}$��1��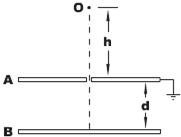 ��ͼ��ʾ��ˮƽ���õ���ƽ�н�����A��B���ɵ�����������ΪC��������Ϊd����ʼʱ����������磬�ô���С��A��ӵأ���A��С�����Ϸ���h��O���д����͵�һ��һ�εص��£���֪�͵�ÿ�ε�����Ϊm������Ϊq����ÿ���䵽B����Ὣ���ȫ������B�壨A����±���Ҳ��ͬʱ��Ӧ�����������ֵ�ɣ��������������ƣ���
��ͼ��ʾ��ˮƽ���õ���ƽ�н�����A��B���ɵ�����������ΪC��������Ϊd����ʼʱ����������磬�ô���С��A��ӵأ���A��С�����Ϸ���h��O���д����͵�һ��һ�εص��£���֪�͵�ÿ�ε�����Ϊm������Ϊq����ÿ���䵽B����Ὣ���ȫ������B�壨A����±���Ҳ��ͬʱ��Ӧ�����������ֵ�ɣ��������������ƣ��� ��ͼ��ABCDΪһ��ֱƽ��Ĺ��������BCˮƽ��A���BC�߳�10�ף�BC��1�ף�AB��CD����⻬��һ����Ϊ1ǧ�˵����壬��A����4��/����ٶȿ�ʼ�˶�������BC���߳�C��10.3m��D���ٶ�Ϊ�㣮��g=10m/s2��
��ͼ��ABCDΪһ��ֱƽ��Ĺ��������BCˮƽ��A���BC�߳�10�ף�BC��1�ף�AB��CD����⻬��һ����Ϊ1ǧ�˵����壬��A����4��/����ٶȿ�ʼ�˶�������BC���߳�C��10.3m��D���ٶ�Ϊ�㣮��g=10m/s2��