题目内容
如图,A、B是在地球大气层外圆周轨道上运行的质量不等的两颗卫星,它们的轨道半径满足RA=2R,RB=3R,R为地球半径,下列说法正确的是( )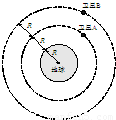
A.A、B的角速度之比ωA:ωB=1:1
B.A、B的线速度之比
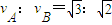
C.A、B的加速度之比a1:a2=3:2
D.A、B受到的万有引力之比FA:FB=9:4
【答案】分析:解:由卫星运动的线速度,角速度,加速度与轨道半径的关系表达式分析比较各量的大小关系.
解答:解:万有引力提供向心力:F向=m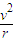 =mω2r=m(
=mω2r=m(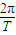 )2r
)2r
因而 G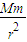 =m
=m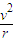 =mω2r=m(
=mω2r=m(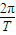 )2r=ma
)2r=ma
解得v=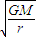 ①T=
①T=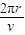 =2π
=2π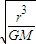 ②ω=
②ω=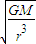 ③a=
③a=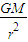 ④
④
A 由ω=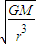 可得ωA:ωB=
可得ωA:ωB=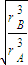 =
=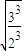 ,故A错误
,故A错误
B 由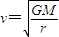 可得vA:vB=
可得vA:vB=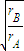 =
=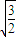 ,故B正确
,故B正确
C 由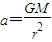 可得a1:a2=
可得a1:a2=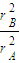 =
=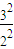 ,故C错误
,故C错误
D 由F=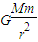 知力还与卫星的质量有关系,而质量关系不明,故D错误
知力还与卫星的质量有关系,而质量关系不明,故D错误
故选:A
点评:考查卫星的运动规律,明确卫星的线速度,角速度,加速度,与半径的关系,会比较不同运动半径的各量的大小关系.
解答:解:万有引力提供向心力:F向=m
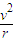 =mω2r=m(
=mω2r=m(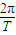 )2r
)2r因而 G
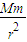 =m
=m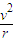 =mω2r=m(
=mω2r=m(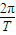 )2r=ma
)2r=ma解得v=
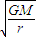 ①T=
①T=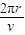 =2π
=2π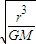 ②ω=
②ω=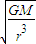 ③a=
③a=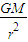 ④
④A 由ω=
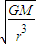 可得ωA:ωB=
可得ωA:ωB=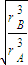 =
=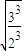 ,故A错误
,故A错误B 由
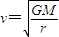 可得vA:vB=
可得vA:vB=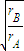 =
=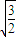 ,故B正确
,故B正确C 由
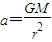 可得a1:a2=
可得a1:a2=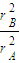 =
=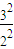 ,故C错误
,故C错误D 由F=
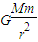 知力还与卫星的质量有关系,而质量关系不明,故D错误
知力还与卫星的质量有关系,而质量关系不明,故D错误故选:A
点评:考查卫星的运动规律,明确卫星的线速度,角速度,加速度,与半径的关系,会比较不同运动半径的各量的大小关系.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 如图,A、B是在地球大气层外圆周轨道上运行的质量不等的两颗卫星,它们的轨道半径满足RA=2R,RB=3R,R为地球半径,下列说法正确的是( )
如图,A、B是在地球大气层外圆周轨道上运行的质量不等的两颗卫星,它们的轨道半径满足RA=2R,RB=3R,R为地球半径,下列说法正确的是( )| A、A、B的角速度之比ωA:ωB=1:1 | ||||
B、A、B的线速度之比vA:vB=
| ||||
| C、A、B的加速度之比a1:a2=3:2 | ||||
| D、A、B受到的万有引力之比FA:FB=9:4 |
 (2011?琼海一模)如图,A、B是在地球大气层外圆周轨道上运行的质量不等的两颗卫星,它们的轨道半径满足RA=2R,RB=3R,R为地球半径,下列说法正确的是( )
(2011?琼海一模)如图,A、B是在地球大气层外圆周轨道上运行的质量不等的两颗卫星,它们的轨道半径满足RA=2R,RB=3R,R为地球半径,下列说法正确的是( )





 如图,A、B是在地球大气层外圆周轨道上运行的质量不等的两颗卫星,它们的轨道半径满足RA=2R,RB=3R,R为地球半径,下列说法正确的是( )
如图,A、B是在地球大气层外圆周轨道上运行的质量不等的两颗卫星,它们的轨道半径满足RA=2R,RB=3R,R为地球半径,下列说法正确的是( )