题目内容
 如图所示,一个小球(视为质点)从H=12m高处由静止开始通过光滑弧形轨道ab进入半径R=4m的竖直圆环,圆环轨道部分的动摩擦因数处处相等,当小球到达顶c时对轨道的压力刚好为零;沿ab滑下后进入光滑弧形轨道bd,且到达高度为h的d点时速度为零,则h值可能为(g取10m/s2)( )
如图所示,一个小球(视为质点)从H=12m高处由静止开始通过光滑弧形轨道ab进入半径R=4m的竖直圆环,圆环轨道部分的动摩擦因数处处相等,当小球到达顶c时对轨道的压力刚好为零;沿ab滑下后进入光滑弧形轨道bd,且到达高度为h的d点时速度为零,则h值可能为(g取10m/s2)( )A.9m
B.8m
C.10m
D.7m
【答案】分析:到达环顶C时,刚好对轨道压力为零,根据牛顿第二定律求出在C点的速度.
根据动能定理研究小球上升到顶点过程求出摩擦力做功.
小球沿轨道下滑,由于机械能有损失,所以下滑速度比上升速度小,因此对轨道压力变小,所受摩擦力变小,所以下滑时,摩擦力做功大小小于上升过程做的功.
根据能量守恒求解.
解答:解:到达环顶C时,刚好对轨道压力为零
所以在C点,重力充当向心力
根据牛顿第二定律
因此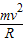 =mg
=mg
R=4m
所以 mv2=2mg
mv2=2mg
所以在C点,小球动能为2mg,因为圆环半径是4m,
因此在C点,以b点为零势能面,小球重力势能=2mgR=8mg
开始小球从H=12m 高处,由静止开始通过光滑弧形轨道ab
因此在小球上升到顶点时,根据动能定理得:
wf+mg(12-8)= mv2-0
mv2-0
所以摩擦力做功wf=-2mg,此时机械能等于10mg,
之后小球沿轨道下滑,由于机械能有损失,所以下滑速度比上升速度小,
因此对轨道压力变小,所受摩擦力变小,所以下滑时,摩擦力做功大小小于2mg,机械能有损失,到达底端时小于10mg
此时小球机械能大于10mg-2mg=8mg,而小于10mg
所以进入光滑弧形轨道bd时,小球机械能的范围为,8mg<Ep<10mg
所以高度范围为8m<h<10m,
故选A.
点评:选取研究过程,运用动能定理解题.动能定理的优点在于适用任何运动包括曲线运动.
了解研究对象的运动过程是解决问题的前提,根据题目已知条件和求解的物理量选择物理规律解决问题.
动能定理的应用范围很广,可以求速度、力、功等物理量,特别是可以去求变力功.
根据动能定理研究小球上升到顶点过程求出摩擦力做功.
小球沿轨道下滑,由于机械能有损失,所以下滑速度比上升速度小,因此对轨道压力变小,所受摩擦力变小,所以下滑时,摩擦力做功大小小于上升过程做的功.
根据能量守恒求解.
解答:解:到达环顶C时,刚好对轨道压力为零
所以在C点,重力充当向心力
根据牛顿第二定律
因此
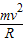 =mg
=mg R=4m
所以
 mv2=2mg
mv2=2mg所以在C点,小球动能为2mg,因为圆环半径是4m,
因此在C点,以b点为零势能面,小球重力势能=2mgR=8mg
开始小球从H=12m 高处,由静止开始通过光滑弧形轨道ab
因此在小球上升到顶点时,根据动能定理得:
wf+mg(12-8)=
 mv2-0
mv2-0所以摩擦力做功wf=-2mg,此时机械能等于10mg,
之后小球沿轨道下滑,由于机械能有损失,所以下滑速度比上升速度小,
因此对轨道压力变小,所受摩擦力变小,所以下滑时,摩擦力做功大小小于2mg,机械能有损失,到达底端时小于10mg
此时小球机械能大于10mg-2mg=8mg,而小于10mg
所以进入光滑弧形轨道bd时,小球机械能的范围为,8mg<Ep<10mg
所以高度范围为8m<h<10m,
故选A.
点评:选取研究过程,运用动能定理解题.动能定理的优点在于适用任何运动包括曲线运动.
了解研究对象的运动过程是解决问题的前提,根据题目已知条件和求解的物理量选择物理规律解决问题.
动能定理的应用范围很广,可以求速度、力、功等物理量,特别是可以去求变力功.

练习册系列答案
相关题目
 如图所示,一个小球沿竖直放置的光滑圆环形轨道做圆周运动,圆环的半径为R,关于小球的运动情况,下列说法中正确的是( )
如图所示,一个小球沿竖直放置的光滑圆环形轨道做圆周运动,圆环的半径为R,关于小球的运动情况,下列说法中正确的是( ) 光滑的水平面上固定着一个螺旋形光滑水平轨道,俯视如图所示.一个小球以一定速度沿轨道切线方向进入轨道,以下关于小球运动的说法中错误的是( )
光滑的水平面上固定着一个螺旋形光滑水平轨道,俯视如图所示.一个小球以一定速度沿轨道切线方向进入轨道,以下关于小球运动的说法中错误的是( ) 如图所示,一个小球在竖直环内至少能做(n+1)次完整的圆周运动,当它第(n-1)次经过环的最低点时速度大小为7m/s,第n次经过环的最低点时的速度大小为5m/s,则小球第(n+1)次经过环的最低点时的速度v的大小一定满足( )
如图所示,一个小球在竖直环内至少能做(n+1)次完整的圆周运动,当它第(n-1)次经过环的最低点时速度大小为7m/s,第n次经过环的最低点时的速度大小为5m/s,则小球第(n+1)次经过环的最低点时的速度v的大小一定满足( ) 光滑的水平面上固定着一个螺旋形光滑水平轨道,俯视如图所示.一个小球以一定速度沿轨道切线方向进入轨道,则轨道对小球做
光滑的水平面上固定着一个螺旋形光滑水平轨道,俯视如图所示.一个小球以一定速度沿轨道切线方向进入轨道,则轨道对小球做 如图所示为一个小球做平抛运动的闪光照片的一部分,图中背景方格的边长均为5cm.如果取g=10m/s2,那么:小球运动中水平分速度的大小是
如图所示为一个小球做平抛运动的闪光照片的一部分,图中背景方格的边长均为5cm.如果取g=10m/s2,那么:小球运动中水平分速度的大小是