题目内容
11. 如图所示,空间存在水平向右的匀强电场.在竖直平面上建立平面直角坐标,在坐标平面的第一象限内固定绝缘光滑的半径为R的$\frac{1}{4}$圆周轨道,轨道的两端在坐标轴上.质量为m的带正电的小球从轨道上端由静止开始滚下,已知重力为电场力的2倍,求:
如图所示,空间存在水平向右的匀强电场.在竖直平面上建立平面直角坐标,在坐标平面的第一象限内固定绝缘光滑的半径为R的$\frac{1}{4}$圆周轨道,轨道的两端在坐标轴上.质量为m的带正电的小球从轨道上端由静止开始滚下,已知重力为电场力的2倍,求:(1)在轨道上小球获得最大速度的位置坐标;
(2)在轨道最低点时轨道对小球的支持力.
分析 (1)当小球在轨道上的速度最大时,设此时小球所在的半径与竖直方向夹角为θ,根据几何关系即可求解;
(2)根据动能定理求出小球运动到最低点的速度,结合牛顿第二定律求出支持力的大小,从而得知小球在B点对轨道的压力.
解答 解:(1)当小球运动到等效最低点时,速度最大,此时小球所处的位置与竖直方向的夹角,与电场力和重力的合力在同一直线上,
由三角形的相似性得:
$\frac{x}{y}=\frac{qE}{mg}$,
x2+y2=R2,
所以:位置坐标($\frac{\sqrt{5}}{5}R,\frac{2\sqrt{5}}{5}R$)
(2)由动能定理得:$mgR-qER=\frac{1}{2}m{v}^{2}$,
由向心力得:${F}_{N}-mg=m\frac{{v}^{2}}{R}$,
所以:FN=2mg.
答:(1)在轨道上小球获得最大速度的位置坐标为($\frac{\sqrt{5}}{5}R,\frac{2\sqrt{5}}{5}R$);
(2)在轨道最低点时轨道对小球的支持力为2mg.
点评 本题综合考查了动能定理、牛顿第二定律,综合性较强,关键掌握小球脱离B点后在水平方向上和竖直方向上的运动规律.

练习册系列答案
相关题目
19. 如图所示,皮带传动装置,皮带轮O和O′上的三点A、B和C,OA=O′C=r,OB=2r,则皮带轮转动时A、B、C三点的情况是( )
如图所示,皮带传动装置,皮带轮O和O′上的三点A、B和C,OA=O′C=r,OB=2r,则皮带轮转动时A、B、C三点的情况是( )
 如图所示,皮带传动装置,皮带轮O和O′上的三点A、B和C,OA=O′C=r,OB=2r,则皮带轮转动时A、B、C三点的情况是( )
如图所示,皮带传动装置,皮带轮O和O′上的三点A、B和C,OA=O′C=r,OB=2r,则皮带轮转动时A、B、C三点的情况是( )| A. | ωA>ωB,VB=VC | B. | ωA=ωB,VB>VC | C. | VA>VB,ωB=ωC | D. | VA=VB,VB>VC |
6.我国第一颗数据中继卫星“天链一号01星”于2008年4月25日在西昌卫星发射中心发射升空,经过4次变轨控制后,于5月1日成功定点在东经77°赤道上空的地球同步轨道.关于成功定点后的“天链一号01星”,下列说法正确的是( )
| A. | 运行速度大于7.9km/s | |
| B. | 离地面高度一定,相对地面静止 | |
| C. | 绕地球运行的角速度比月球绕地球运行的角速度大 | |
| D. | 向心加速度与静止在地球表面赤道上物体的向心加速度大小相等 |
16. a、b、c三个物体在同一条直线上运动,三个物体的x-t图象如图所示,c是一条抛物线,坐标原点是抛物线的顶点,下列说法中正确的是( )
a、b、c三个物体在同一条直线上运动,三个物体的x-t图象如图所示,c是一条抛物线,坐标原点是抛物线的顶点,下列说法中正确的是( )
 a、b、c三个物体在同一条直线上运动,三个物体的x-t图象如图所示,c是一条抛物线,坐标原点是抛物线的顶点,下列说法中正确的是( )
a、b、c三个物体在同一条直线上运动,三个物体的x-t图象如图所示,c是一条抛物线,坐标原点是抛物线的顶点,下列说法中正确的是( )| A. | a、b两物体都做匀速直线运动,且两个物体的速度相同 | |
| B. | a、b两物体都做匀速直线运动,且两个物体的速度大小相等,方向相反 | |
| C. | 当t=5s时,a、b两个物体相距最近 | |
| D. | 物体c做变速直线运动 |
20. 如图所示,有同学做实验时不慎将圆柱形试管塞卡于试管底部,该试管塞中轴穿孔.为了拿出试管塞而不损坏试管,该同学紧握试管让其倒立由静止开始竖直向下做匀加速直线运动,t=0.20s后立即停止,此时试管下降H=0.80m,试管塞将恰好能从试管口滑出.已知试管总长L=21.0cm,底部球冠的高度h=1.0cm,试管塞的长度为d=2.0cm,设试管塞相对试管壁滑动时受到的摩擦力恒定,不计空气阻力,重力加速度g=l0m/s2.则以下说法正确的是( )
如图所示,有同学做实验时不慎将圆柱形试管塞卡于试管底部,该试管塞中轴穿孔.为了拿出试管塞而不损坏试管,该同学紧握试管让其倒立由静止开始竖直向下做匀加速直线运动,t=0.20s后立即停止,此时试管下降H=0.80m,试管塞将恰好能从试管口滑出.已知试管总长L=21.0cm,底部球冠的高度h=1.0cm,试管塞的长度为d=2.0cm,设试管塞相对试管壁滑动时受到的摩擦力恒定,不计空气阻力,重力加速度g=l0m/s2.则以下说法正确的是( )
 如图所示,有同学做实验时不慎将圆柱形试管塞卡于试管底部,该试管塞中轴穿孔.为了拿出试管塞而不损坏试管,该同学紧握试管让其倒立由静止开始竖直向下做匀加速直线运动,t=0.20s后立即停止,此时试管下降H=0.80m,试管塞将恰好能从试管口滑出.已知试管总长L=21.0cm,底部球冠的高度h=1.0cm,试管塞的长度为d=2.0cm,设试管塞相对试管壁滑动时受到的摩擦力恒定,不计空气阻力,重力加速度g=l0m/s2.则以下说法正确的是( )
如图所示,有同学做实验时不慎将圆柱形试管塞卡于试管底部,该试管塞中轴穿孔.为了拿出试管塞而不损坏试管,该同学紧握试管让其倒立由静止开始竖直向下做匀加速直线运动,t=0.20s后立即停止,此时试管下降H=0.80m,试管塞将恰好能从试管口滑出.已知试管总长L=21.0cm,底部球冠的高度h=1.0cm,试管塞的长度为d=2.0cm,设试管塞相对试管壁滑动时受到的摩擦力恒定,不计空气阻力,重力加速度g=l0m/s2.则以下说法正确的是( )| A. | 试管塞从静止开始到离开试管口的总位移为1.0 m | |
| B. | 试管塞从静止开始到离开试管口的总时间为0.25s | |
| C. | 试管塞将要从试管口滑出时的加速度大小为40m/s2 | |
| D. | 试管塞受到的滑动摩擦力与其重力的比值为16:1 |
1.如图为一列沿x轴负方向传播的简谐横波在t=0时的波形图,当Q点的振动状态传至P点时,则( )


| A. | Q点处于波峰位置 | |
| B. | Q点的加速度沿Y轴正方向 | |
| C. | Q点的振动速度比P点的大 | |
| D. | 1cm<x<3cm范围内的质点均沿Y轴负方向运动 |
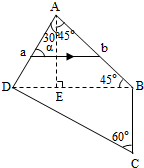 如图所示,玻璃棱镜ABCD可以看成是由△ADE,△ABE,△BCD三个直角三棱镜组成,一束频率f=5.3×1014Hz的单色光束从AD面入射,在棱镜中的折射光线如图中ab所示,ab与AD面的夹角α=60°,已知光在真空中的速度c=3×108m/s,玻璃的折射率n=1.5,求:
如图所示,玻璃棱镜ABCD可以看成是由△ADE,△ABE,△BCD三个直角三棱镜组成,一束频率f=5.3×1014Hz的单色光束从AD面入射,在棱镜中的折射光线如图中ab所示,ab与AD面的夹角α=60°,已知光在真空中的速度c=3×108m/s,玻璃的折射率n=1.5,求: