题目内容
静止的镭226(88226Ra)发生α衰变,生成氡(Rn),如果衰变中放出的能量都转化为α粒子和氡核的动能.(1)写出衰变方程;
(2)求α粒子与氡核的动能之比;
(3)若α粒子与氡核的运动方向与匀强磁场的方向垂直,画出轨迹示意图,并计算轨道半径之比.
【答案】分析:(1)由质数和核电荷数守恒写核反应方程.(2)由动量守恒知速度之比,再求动能之比.(3)由动量守恒定律和半径公式求半径之比.
解答:解:(1)22688Ra→42He+22286Rn
(2)生成的原子核动量守恒,设α粒子质量为m,氡的质量为M,
由MV=mv 知V:v′=m:M=4:222=2:111
知V:v′=m:M=4:222=2:111
则: mv′2:
mv′2: MV2=
MV2= ×4×1112:
×4×1112: ×222×22=111:2
×222×22=111:2
(3)α粒子与氡核在匀强磁场中做方向相反的匀速圆周运动,
则由:r=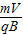 知半径与电荷数成反比
知半径与电荷数成反比
所以rα:rRn=qRn:qα=86:2=43:1
点评:本题考查了核反应方程,和动量守恒定律,关键是知道谁和谁动量守恒及粒子在匀强磁场中的运动情况.
解答:解:(1)22688Ra→42He+22286Rn
(2)生成的原子核动量守恒,设α粒子质量为m,氡的质量为M,
由MV=mv
 知V:v′=m:M=4:222=2:111
知V:v′=m:M=4:222=2:111则:
 mv′2:
mv′2: MV2=
MV2= ×4×1112:
×4×1112: ×222×22=111:2
×222×22=111:2(3)α粒子与氡核在匀强磁场中做方向相反的匀速圆周运动,
则由:r=
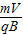 知半径与电荷数成反比
知半径与电荷数成反比所以rα:rRn=qRn:qα=86:2=43:1
点评:本题考查了核反应方程,和动量守恒定律,关键是知道谁和谁动量守恒及粒子在匀强磁场中的运动情况.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (选修模块3-5)
(选修模块3-5)