题目内容
19.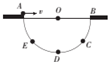 如图所示,有一半球形容器,其竖直截面为半圆.AB为沿水平方向的直径,D是圆周的最低点,E是AD间某一点,C与E在相同的高度.一个可视为质点的小球从A点以速度v0水平抛出,恰好落在E点,若以2v0抛出,恰好落在C点,设球的半径为R,则下列判断正确的是( )
如图所示,有一半球形容器,其竖直截面为半圆.AB为沿水平方向的直径,D是圆周的最低点,E是AD间某一点,C与E在相同的高度.一个可视为质点的小球从A点以速度v0水平抛出,恰好落在E点,若以2v0抛出,恰好落在C点,设球的半径为R,则下列判断正确的是( )| A. | 初速度为$\frac{3{v}_{0}}{2}$时,小球恰好落在D点 | |
| B. | 初速度为$\frac{3{v}_{0}}{2}$时,小球将落在D点的左侧 | |
| C. | OC与竖直方向夹角的正弦值为$\frac{1}{4}$ | |
| D. | OE与竖直方向夹角的正弦值为$\frac{1}{3}$ |
分析 平抛运动可以分解为在水平方向上的匀速直线运动,和竖直方向上的自由落体运动,
竖直方向上的位移已经知道了,但是水平方向的位移要用三角形的知识来求,然后才能求圆的半径.
解答 解:设圆半径为r,质点做平抛运动,设水平方向的位移为x,竖直方向上的位移为y,
则:x=v0t
由于恰好落在C点时的初速度是恰好落在E点时的初速度的2倍,所以:
xAC=2xAE
连接OC和OE,由于CE在同一条水平线上,由几何关系可知它们与竖直方向之间的夹角相等,设为θ,如图:
则:r+rsinθ=2(r-rcosθ)
所以:sinθ=$\frac{1}{3}$;所以选项C错误,D正确;
$\frac{1}{2}{x}_{AC}={x}_{AE}=\frac{2}{3}r$
由图可知D点的位置在CE点的下方,由:y=$\frac{1}{2}g{t}^{2}$可知,小球到达D点的时间大于到达CE的时间;
若小球初速度为$\frac{3{v}_{0}}{2}$时,小球落在CE点之间时的位移:$x=v′t′=\frac{3{v}_{0}}{2}•t′>\frac{3{v}_{0}}{2}•t$=$\frac{3{v}_{0}}{2}•\frac{\frac{2}{3}r}{{v}_{0}}=r$
所以若小球初速度为$\frac{3{v}_{0}}{2}$时,小球落在D点的右侧.故A错误,B错误.
故选:D
点评 考查平抛运动规律的应用,但是水平方向的位移不知道,所以用的数学的知识较多,需要熟练的应用三角形的边角关系.

练习册系列答案
相关题目
9. 如图所示,用实线表示某一电场电场线的分布情况,一带电粒子在电场的运动轨迹如图中虚线所示.粒子只受电场力作用,则下列说法正确的是( )
如图所示,用实线表示某一电场电场线的分布情况,一带电粒子在电场的运动轨迹如图中虚线所示.粒子只受电场力作用,则下列说法正确的是( )
 如图所示,用实线表示某一电场电场线的分布情况,一带电粒子在电场的运动轨迹如图中虚线所示.粒子只受电场力作用,则下列说法正确的是( )
如图所示,用实线表示某一电场电场线的分布情况,一带电粒子在电场的运动轨迹如图中虚线所示.粒子只受电场力作用,则下列说法正确的是( )| A. | 若粒子是从A运动到B,则粒子带正电 | |
| B. | 无论粒子沿哪一个方向运动,粒子都带负电 | |
| C. | 若粒子是从A运动到B,则其加速度增大 | |
| D. | 若粒子是从A运动到B,则其电势能增大 |
10.浙江临海括苍山风电场部装机33台,其中1号风场10台,2号风场7台,3台风场16台,总容量1.98×107W.在家电中待机能耗较大是电视机,现阶段我国平板电视保有量达到2.5亿台,平均每台待机功率为8W.请估算括苍山风电场发电多久可供全国的平板电视待电视待机一天( )
| A. | 一天 | B. | 一个月 | C. | 一百天 | D. | 一年 |
8. 2010年,上海成功举办盛大的世界博览会.回眸一下历届世博会,很多科技成果从世博会上走向世界.例如:1873年奥地利维也纳世博会上,线路意外搭错造就“偶然发明”,导致发电机变成了电动机.如图所示,是著名的电磁旋转实验,这一装置实际上就是最早的电动机.图中A是可动磁铁,B是固定导线,C是可动导线,D是固定磁铁.图中黑色部分表示汞(磁铁和导线的下半部分都浸没在汞中),下部接在电源上.请你判断这时自上向下看,A和C转动方向为( )
2010年,上海成功举办盛大的世界博览会.回眸一下历届世博会,很多科技成果从世博会上走向世界.例如:1873年奥地利维也纳世博会上,线路意外搭错造就“偶然发明”,导致发电机变成了电动机.如图所示,是著名的电磁旋转实验,这一装置实际上就是最早的电动机.图中A是可动磁铁,B是固定导线,C是可动导线,D是固定磁铁.图中黑色部分表示汞(磁铁和导线的下半部分都浸没在汞中),下部接在电源上.请你判断这时自上向下看,A和C转动方向为( )
 2010年,上海成功举办盛大的世界博览会.回眸一下历届世博会,很多科技成果从世博会上走向世界.例如:1873年奥地利维也纳世博会上,线路意外搭错造就“偶然发明”,导致发电机变成了电动机.如图所示,是著名的电磁旋转实验,这一装置实际上就是最早的电动机.图中A是可动磁铁,B是固定导线,C是可动导线,D是固定磁铁.图中黑色部分表示汞(磁铁和导线的下半部分都浸没在汞中),下部接在电源上.请你判断这时自上向下看,A和C转动方向为( )
2010年,上海成功举办盛大的世界博览会.回眸一下历届世博会,很多科技成果从世博会上走向世界.例如:1873年奥地利维也纳世博会上,线路意外搭错造就“偶然发明”,导致发电机变成了电动机.如图所示,是著名的电磁旋转实验,这一装置实际上就是最早的电动机.图中A是可动磁铁,B是固定导线,C是可动导线,D是固定磁铁.图中黑色部分表示汞(磁铁和导线的下半部分都浸没在汞中),下部接在电源上.请你判断这时自上向下看,A和C转动方向为( )| A. | 可动磁铁A转动方向为逆时针 | B. | A和C转动方向均为逆时针 | ||
| C. | 可动导线C转动方向为顺时针 | D. | A和C转动方向均为顺时针 |
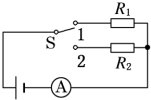 如图所示,定值电阻R1=10Ω,R2=8Ω,当开关S接“1”时,电流表示数为0.20A,那么当S接“2”时,电流表示数为0.24A.求电源的电动势和内阻.
如图所示,定值电阻R1=10Ω,R2=8Ω,当开关S接“1”时,电流表示数为0.20A,那么当S接“2”时,电流表示数为0.24A.求电源的电动势和内阻.
 某物理兴趣小组的同学为了验证在竖直面内做圆周运动的物体在最低点受到的拉力与根据学过的物理规律计算出拉力是否相同,设计了如图所示的实验,一根轻绳一端固定在O点,另一端系着一个小球,他在绳的固定点O安装了一个拉力传感器来测量绳拉力的大小.他们首先在最低点给小球一适当大小的初速度,使小球运动到最高点时,拉力传感器的示数为零,最后记录下当小球运动到最低点时拉力传感器的示数T.
某物理兴趣小组的同学为了验证在竖直面内做圆周运动的物体在最低点受到的拉力与根据学过的物理规律计算出拉力是否相同,设计了如图所示的实验,一根轻绳一端固定在O点,另一端系着一个小球,他在绳的固定点O安装了一个拉力传感器来测量绳拉力的大小.他们首先在最低点给小球一适当大小的初速度,使小球运动到最高点时,拉力传感器的示数为零,最后记录下当小球运动到最低点时拉力传感器的示数T. 如图所示,在大小为E,方向竖直向上的匀强电场中,长为L的轻绳一端固定在O点,另一端拴一个带电荷量+q的小球,已知qE=3mg,要使球能在竖直平面内做完整的圆周运动,球在A点的最小速度应为多大?
如图所示,在大小为E,方向竖直向上的匀强电场中,长为L的轻绳一端固定在O点,另一端拴一个带电荷量+q的小球,已知qE=3mg,要使球能在竖直平面内做完整的圆周运动,球在A点的最小速度应为多大?