题目内容
1.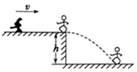 如图所示,高为h=0.8m的平台上,覆盖一层薄冰,现有一质量为50kg的滑雪爱好者,以一定的初速度向平台边缘滑去,着地前的速度方向与水平地面的夹角为45°.将滑雪者视为质点.g取10m/s2.求
如图所示,高为h=0.8m的平台上,覆盖一层薄冰,现有一质量为50kg的滑雪爱好者,以一定的初速度向平台边缘滑去,着地前的速度方向与水平地面的夹角为45°.将滑雪者视为质点.g取10m/s2.求(1)在空中运动的时间
(2)离开平台边缘时的速度大小
(3)着地点到平台边缘的水平距离.
分析 根据平抛运动的高度求出运动的时间,结合速度时间公式求出竖直分速度,通过平行四边形定则求出滑雪者离开平台的速度.根据初速度和时间求出水平位移.
解答 解:(1)根据$h=\frac{1}{2}g{t}_{\;}^{2}$,得:
$t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×0.8}{10}}=0.4s$
(2)落地时竖直分速为:
度${v}_{y}^{\;}=gt=10×0.4=4m/s$
根据题意落地时速度与水平方向的夹角为45°,则有:
$tan45°=\frac{{v}_{y}^{\;}}{{v}_{o}^{\;}}$
解得:${v}_{0}^{\;}=4m/s$
(3)根据水平位移的公式有:$x={v}_{0}^{\;}t=4×0.4m=1.6m$
答:(1)在空中运动的时间0.4s
(2)离开平台边缘时的速度大小4m/s
(3)着地点到平台边缘的水平距离1.6m.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.由牛顿第二定律F=ma可知( )
| A. | 物体的加速度跟质量成反比 | |
| B. | 物体的加速度与物体受到的合外力方向一致 | |
| C. | F是指物体所受的合外力 | |
| D. | 力是物体产生加速度的原因 |
16.据英国《卫报》网站2015年1月6日报道,在太阳系之外,科学家发现了一颗最适宜人类居住的类地行星,绕恒星橙矮星运行,命名为“开普勒438b”.假设该行星绕橙矮星的运动与地球绕太阳的运动均视为匀速圆周运动,该行星运行的周期为地球运行周期的p倍,橙矮星的质量为太阳的q倍.则该行星与地球的( )
| A. | 轨道半径之比为$\root{3}{{p}^{2}q}$ | B. | 轨道半径之比为$\root{3}{{p}^{2}}$ | ||
| C. | 线速度之比为 $\root{3}{\frac{q}{p}}$ | D. | 线速度之比为 $\sqrt{\frac{1}{p}}$ |
6.下列关于重力的说法正确的是( )
| A. | 重力的方向不一定竖直向下 | |
| B. | 重力就是物体受到地球的吸引力 | |
| C. | 物体的重心不一定在物体上 | |
| D. | 同一个物体在赤道和北极所受重力相同 |
13. 如图所示,从地面上方某点,将一小球以10m/s的初速度沿水平方向抛出,小球经1s落地,不计空气阻力,g取10m/s2,则可求出( )
如图所示,从地面上方某点,将一小球以10m/s的初速度沿水平方向抛出,小球经1s落地,不计空气阻力,g取10m/s2,则可求出( )
 如图所示,从地面上方某点,将一小球以10m/s的初速度沿水平方向抛出,小球经1s落地,不计空气阻力,g取10m/s2,则可求出( )
如图所示,从地面上方某点,将一小球以10m/s的初速度沿水平方向抛出,小球经1s落地,不计空气阻力,g取10m/s2,则可求出( )| A. | 小球抛出点离地面的高度为5 m | |
| B. | 小球抛出点到落地点的水平距离为10 m | |
| C. | 小球落地点的速度大小为20 m/s | |
| D. | 小球落地时的速度方向与水平地面成60°角 |
10. 质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
 质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )| A. | 重力势能增加了mgh | B. | 克服摩擦力做功$\frac{1}{4}$mgh | ||
| C. | 动能损失了mgh | D. | 机械能损失了$\frac{1}{2}$mgh |
6. 如图所示,与水平地面夹角为锐角的下面低端A向上有三个等间距点B、C和D,即AB=BC=CD.小滑块P以初速v从A出发,沿斜面向上运动.先设置斜面与滑块间处处无摩擦,则滑块到达D位置刚好停下,而后下滑.若设置斜面 AB部分与滑块间有处处相同的摩擦,其余部位与滑块间仍无摩擦,则滑块上行到C位置刚好停下,而后下滑.滑块下滑到B位置时速度以及回到 A端时速度大小分别为( )
如图所示,与水平地面夹角为锐角的下面低端A向上有三个等间距点B、C和D,即AB=BC=CD.小滑块P以初速v从A出发,沿斜面向上运动.先设置斜面与滑块间处处无摩擦,则滑块到达D位置刚好停下,而后下滑.若设置斜面 AB部分与滑块间有处处相同的摩擦,其余部位与滑块间仍无摩擦,则滑块上行到C位置刚好停下,而后下滑.滑块下滑到B位置时速度以及回到 A端时速度大小分别为( )
 如图所示,与水平地面夹角为锐角的下面低端A向上有三个等间距点B、C和D,即AB=BC=CD.小滑块P以初速v从A出发,沿斜面向上运动.先设置斜面与滑块间处处无摩擦,则滑块到达D位置刚好停下,而后下滑.若设置斜面 AB部分与滑块间有处处相同的摩擦,其余部位与滑块间仍无摩擦,则滑块上行到C位置刚好停下,而后下滑.滑块下滑到B位置时速度以及回到 A端时速度大小分别为( )
如图所示,与水平地面夹角为锐角的下面低端A向上有三个等间距点B、C和D,即AB=BC=CD.小滑块P以初速v从A出发,沿斜面向上运动.先设置斜面与滑块间处处无摩擦,则滑块到达D位置刚好停下,而后下滑.若设置斜面 AB部分与滑块间有处处相同的摩擦,其余部位与滑块间仍无摩擦,则滑块上行到C位置刚好停下,而后下滑.滑块下滑到B位置时速度以及回到 A端时速度大小分别为( )| A. | $\frac{v}{2}$、$\frac{\sqrt{3}v}{3}$ | B. | $\frac{\sqrt{3}v}{3}$、$\frac{\sqrt{3}v}{3}$ | C. | $\frac{v}{2}$、$\frac{\sqrt{3}v}{2}$ | D. | $\frac{v}{2}$、$\frac{v}{2}$ |
