题目内容
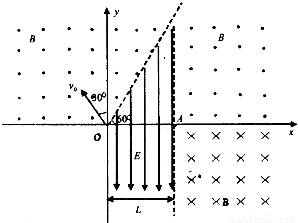
在竖直平面内,以虚线为界分布着如图所示的匀强电场和足够大的匀强磁场,各区域磁场的磁感应强度大小均为B,匀强电场方向竖直向下,大小为E=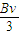 ;倾斜虚线与x轴之间的夹角为60°,一带正电的C粒子从O点以速度v与y轴成30°角射入左侧磁场,粒子经过倾斜虚线后进入匀强电场,恰好从图中A点射入右侧x轴下方磁场.已知带正电粒子的电荷量为q,质量为m(粒子重力忽略不计).试求:
;倾斜虚线与x轴之间的夹角为60°,一带正电的C粒子从O点以速度v与y轴成30°角射入左侧磁场,粒子经过倾斜虚线后进入匀强电场,恰好从图中A点射入右侧x轴下方磁场.已知带正电粒子的电荷量为q,质量为m(粒子重力忽略不计).试求:(1)带电粒子通过倾斜虚线时的位置坐标;
(2)粒子到达A点时速度的大小和方向以及匀强电场的宽度L;
(3)若在C粒子从O点出发的同时,一不带电的D粒子从A点以速度v沿x轴正方向匀速运动,最终两粒子相碰,求D粒子速度v的可能值.
【答案】分析:(1)根据洛伦兹力提供向心力,由牛顿第二定律可解出轨迹半径.再由几何知识来算出位置的坐标;
(2)由几何关系得知,粒子进入匀强电场做类平抛运动,因此可将其运动分解,根据牛顿第二定律与运动学公式去确定到达A点时速度的大小和方向,再由运动学位移公式求出匀强电场的宽度;
(3)根据几何知识,得出C粒子在左侧磁场运动轨迹为 圆周,而C粒子在右侧磁场运动轨迹可能为多个
圆周,而C粒子在右侧磁场运动轨迹可能为多个 圆弧,从而由周期公式可算出C粒子到达x轴时可能运动时间;再由运动轨迹半径公式来确定粒子运动的可能距离,从而求出粒子速度的可能值.
圆弧,从而由周期公式可算出C粒子到达x轴时可能运动时间;再由运动轨迹半径公式来确定粒子运动的可能距离,从而求出粒子速度的可能值.
解答:解:(1)洛伦兹力提供向心力,则有: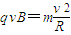
解得: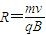
由几何知识,则有: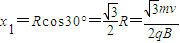
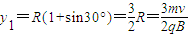
所以位置坐标为:(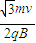 ,
,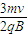 )
)
(2)由几何关系可知粒子垂直电场线进入匀强电场做类平抛运动
牛顿第二定律,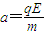
运动学公式,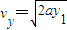
粒子到达A点的速度大小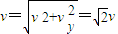
设速度与x轴的夹角为θ,则: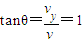 ,
,
解得,θ=45°
由vy=at1
解得: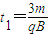
x2=vt1
联立以上各式解得: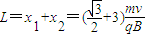
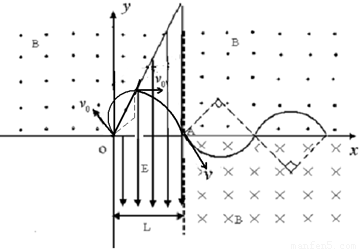
(3)粒子在磁场中运动周期: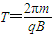
由几何关系可知,C粒子在左侧磁场运动轨迹为 圆周,运动时间
圆周,运动时间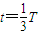
由几何关系可知,C粒子在右侧磁场运动轨迹可能为多个 圆弧,
圆弧,
如图,C粒子到达x轴时可能运动时间: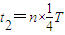 (n=1,2,3…)
(n=1,2,3…)
C粒子在右侧磁场运动轨迹半径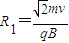
D粒子在x轴与C粒子相遇距A点的可能距离: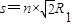 (n=1、2、3…)
(n=1、2、3…)
所以,D粒子速度v的可能值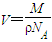 =
=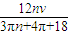 (n=1,2,3…)
(n=1,2,3…)
答:(1)带电粒子通过倾斜虚线时的位置坐标为:(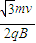 ,
,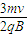 );
);
(2)粒子到达A点时速度的大小为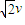 和方向与x轴成45°,电强电场的宽度为
和方向与x轴成45°,电强电场的宽度为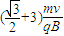 ;
;
(3)若在C粒子从O点出发的同时,一不带电的D粒子从A点以速度v沿x轴正方向匀速运动,最终两粒子相碰,则D粒子速度v的可能值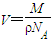 =
=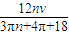 (n=1,2,3…).
(n=1,2,3…).
点评:考查了仅仅由电场力做类平抛运动,还有仅仅由洛伦兹力提供向心力做匀速圆周运动,学会如何处理类平抛运动及匀速圆周运动的问题,形成一定的解题能力.同时注意几何知识的熟练应用,并强调洛伦兹力的方向的重要性及运动轨迹的多样性.
(2)由几何关系得知,粒子进入匀强电场做类平抛运动,因此可将其运动分解,根据牛顿第二定律与运动学公式去确定到达A点时速度的大小和方向,再由运动学位移公式求出匀强电场的宽度;
(3)根据几何知识,得出C粒子在左侧磁场运动轨迹为
 圆周,而C粒子在右侧磁场运动轨迹可能为多个
圆周,而C粒子在右侧磁场运动轨迹可能为多个 圆弧,从而由周期公式可算出C粒子到达x轴时可能运动时间;再由运动轨迹半径公式来确定粒子运动的可能距离,从而求出粒子速度的可能值.
圆弧,从而由周期公式可算出C粒子到达x轴时可能运动时间;再由运动轨迹半径公式来确定粒子运动的可能距离,从而求出粒子速度的可能值.解答:解:(1)洛伦兹力提供向心力,则有:
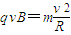
解得:
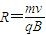
由几何知识,则有:
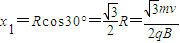
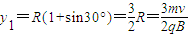
所以位置坐标为:(
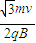 ,
,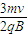 )
)(2)由几何关系可知粒子垂直电场线进入匀强电场做类平抛运动
牛顿第二定律,
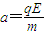
运动学公式,
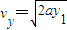
粒子到达A点的速度大小
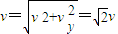
设速度与x轴的夹角为θ,则:
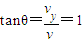 ,
,解得,θ=45°
由vy=at1
解得:
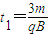
x2=vt1
联立以上各式解得:
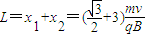
(3)粒子在磁场中运动周期:
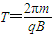

由几何关系可知,C粒子在左侧磁场运动轨迹为
 圆周,运动时间
圆周,运动时间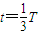
由几何关系可知,C粒子在右侧磁场运动轨迹可能为多个
 圆弧,
圆弧,如图,C粒子到达x轴时可能运动时间:
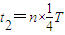 (n=1,2,3…)
(n=1,2,3…)C粒子在右侧磁场运动轨迹半径
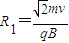
D粒子在x轴与C粒子相遇距A点的可能距离:
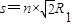 (n=1、2、3…)
(n=1、2、3…)所以,D粒子速度v的可能值
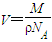 =
=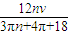 (n=1,2,3…)
(n=1,2,3…) 答:(1)带电粒子通过倾斜虚线时的位置坐标为:(
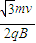 ,
,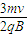 );
);(2)粒子到达A点时速度的大小为
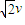 和方向与x轴成45°,电强电场的宽度为
和方向与x轴成45°,电强电场的宽度为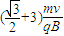 ;
;(3)若在C粒子从O点出发的同时,一不带电的D粒子从A点以速度v沿x轴正方向匀速运动,最终两粒子相碰,则D粒子速度v的可能值
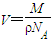 =
=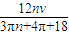 (n=1,2,3…).
(n=1,2,3…).点评:考查了仅仅由电场力做类平抛运动,还有仅仅由洛伦兹力提供向心力做匀速圆周运动,学会如何处理类平抛运动及匀速圆周运动的问题,形成一定的解题能力.同时注意几何知识的熟练应用,并强调洛伦兹力的方向的重要性及运动轨迹的多样性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
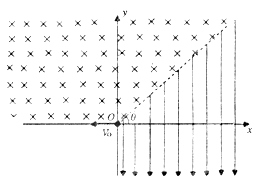
 (2011?株洲一模)在竖直平面内,以虚线为界分布着如图所示的匀强电场和匀强磁场,其中匀强电场方向向下,大小为E;匀强磁场垂直纸面向里,磁感应强度大小为B.虚线与水平线之间的夹角为θ=45°,一带电粒子以速度v0水平射入匀强磁场,已知带负电粒子电荷量为q,质量为m,(重力忽略不计,电场、磁场区域足够大).
(2011?株洲一模)在竖直平面内,以虚线为界分布着如图所示的匀强电场和匀强磁场,其中匀强电场方向向下,大小为E;匀强磁场垂直纸面向里,磁感应强度大小为B.虚线与水平线之间的夹角为θ=45°,一带电粒子以速度v0水平射入匀强磁场,已知带负电粒子电荷量为q,质量为m,(重力忽略不计,电场、磁场区域足够大).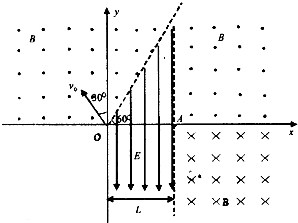 在竖直平面内,以虚线为界分布着如图所示的匀强电场和足够大的匀强磁场,各区域磁场的磁感应强度大小均为B,匀强电场方向竖直向下,大小为E=
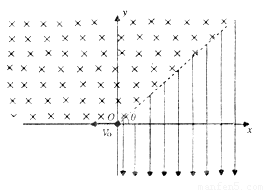
在竖直平面内,以虚线为界分布着如图所示的匀强电场和足够大的匀强磁场,各区域磁场的磁感应强度大小均为B,匀强电场方向竖直向下,大小为E=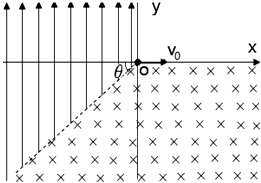 在竖直平面内,以虚线为界分布着如图所示的匀强电场和匀强磁场,其中匀强电场方向向上,大小为E;匀强磁场垂直纸面向里,磁感应强度大小为B.虚线与水平线之间的夹角为θ=45°,一带电粒子从O点以速度v0水平射入匀强磁场,已知带负电粒子电荷量为q,质量为m,(重力忽略不计,电场、磁场区域足够大).
在竖直平面内,以虚线为界分布着如图所示的匀强电场和匀强磁场,其中匀强电场方向向上,大小为E;匀强磁场垂直纸面向里,磁感应强度大小为B.虚线与水平线之间的夹角为θ=45°,一带电粒子从O点以速度v0水平射入匀强磁场,已知带负电粒子电荷量为q,质量为m,(重力忽略不计,电场、磁场区域足够大).